An acoustic signature of extreme failure on model granular materials

Abstract

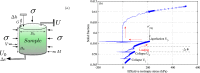
Unexpectedly, granular materials can fail, the structure even destroyed, spontaneously in simple isotropic compression with stick-slip-like frictional behaviour. This extreme behaviour is conceptually impossible for saturated two-phase assembly in classical granular physics. Furthermore, the triggering mechanisms of these laboratory events remain mysterious, as in natural earthquakes. Here, we report a new interpretation of these failures in under-explored isotropic compression using the time-frequency analysis of Cauchy continuous wavelet transform of acoustic emissions and multiphysics numerical simulations. Wavelet transformation techniques can give insights into the temporal evolution of the state of granular materials en route to failure and offer a plausible explanation of the distinctive hearing sound of the stick-slip phenomenon. We also extend the traditional statistical seismic Gutenberg-Richter power-law behaviour for hypothetical biggest earthquakes based on the mechanisms of stick-slip frictional instability, using very large artificial isotropic labquakes and the ultimate unpredictable liquefaction failure.

Figure 1

Dynamic instabilities of model granular materials in drained isotropic compression. (a) Sketch of the experimental setup of the drained isotropic compression on cylindrical sample inside a triaxial cell. The axial displacement $\mathrm{\Delta }h$ and the water volume $\mathrm{\Delta }v$ were measured to estimate the global axial strain ${\epsilon }_a$ and solid fraction $\mathrm{\Phi }$. The back pressure $U_0$ was applied at the sample bottom, while the measurements of static pore-water pressure U at the sample top permit to assess the homogeneity of the effective stress state. One piezoelectric accelerometer measures the vertical acceleration G of the sample top cap. One complementary non-contact portable laser vibrometer V and one microphone M record the lateral surface vibration and the radial sound pressure outside the triaxial chamber. (b) Collapses ${\text{U}}_1$, ${\text{U}}_2$ and liquefaction ${\text{U}}_3$ in isotropic drained compression from 20 up to 212 kPa of confining pressure. Red arrows denote the direction of loading.

Figure 2

Typical temporal evolution of isotropic collapse ${\text{U}}_2$ (blue) and liquefaction ${\text{U}}_3$ (red) on 0.7 mm CVP beads in isotropic drained compression: successively vertical top cap acceleration, normalised excess pore pressure, permanent incremental axial and volumetric strain. The superimposed liquefaction points (solid circles) on normalised excess pore pressure, with systematic time delay (vertical black dashed line), are above the unity level, indicating non-liquefaction event for collapse ${\text{U}}_2$. The axial strain of collapse event is magnified by a factor of 30. A small aftershock (inset figures), without affecting the liquefaction results, occurs after 5 s.

Figure 3

Spectrogram $|T_{\psi }(f,t-t_i){|}^2$ using Continuous Cauchy Wavelet Transform on a segment of non-stationary signal of 10 s of vertical acceleration in isotropic liquefaction $U_3$ at 212 kPa (top). Details of spectrogram (left) and multiphysics numerical simulation (right) on 1175 Hz (top), 253 Hz of solid isotropic linear elastic medium (middle), 5 Hz of thin latex membrane (bottom).

Figure 4

Continuous Cauchy wavelet transformation of the excess pore fluid pressure or intergranular stress with full destruction of saturated granular assembly (isotropic liquefaction $U_3$) at 212 kPa of confining pressure.

Figure 5

Probability density distribution of acoustic energy $E_a$ of the vertical top cap acceleration for isotropic collapses (solid symbols) and liquefactions (large hollow red diamonds) events. The blue dashed line represents the power-law behaviour, $P(E_a)\sim E_a^{-\beta }$, $\beta$ = 1.21 ± 0.01, R${}^2$ = 0.967. The symbol ± stands for 95% confidence interval.