Non-Abelian anyon collider

Abstract

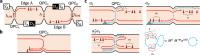
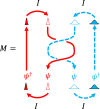
A collider where particles are injected onto a beam splitter from opposite sides has been used for identifying quantum statistics of identical particles. The collision leads to bunching of the particles for bosons and antibunching for fermions. In recent experiments, a collider was applied to a fractional quantum Hall regime hosting Abelian anyons. The observed negative cross-correlation of electrical currents cannot be understood with fermionic antibunching. Here we predict, based on a conformal field theory and a non-perturbative treatment of non-equilibrium anyon injection, that the collider provides a tool for observation of the braiding statistics of various Abelian and non-Abelian anyons. Its dominant process is not direct collision between injected anyons, contrary to common expectation, but braiding between injected anyons and an anyon excited at the collider. The dependence of the resulting negative cross-correlation on the injection currents distinguishes non-Abelian SU(2)_k anyons, Ising anyons, and Abelian Laughlin anyons.

Fig. 1. Fractional quantum Hall collider.

a Setup. Anyons are injected to Edge A/B through QPC_A/B by voltage V_A/B,inj applied to Source S_A/B, accompanied by current I_A/B,inj of charge e^*. The injected anyons (red narrow peaks) flow downstream to QPC_C (red trajectories); a corresponding setup for upstream anyons is shown in Fig. 2. The QPCs are in a weak backscattering regime. b Conventional collision where an injected anyon collides with another after tunneling at QPC_C. c Time-domain interference involving (n, m) braiding. Its subprocesses a₁ and a₂ share the common spatial locations of injected anyons on the Edges. They have tunneling of an additional anyon at QPC_C (blue wide peaks for the anyon, white peaks for its hole counterpart) by thermal or quantum fluctuations, but at different times (blue trajectories). In a₁ (resp. a₂), the tunneling happens after (resp. before) n and m injected anyons pass QPC_C on Edges A and B. In their interference $a_2^{*}{a}_1$, the additional anyon braids the injected anyons, depicted as a blue twisted loop topologically linked with n “counterclockwise” and m “clockwise” red loops. Untying and untwisting the loops give monodromy $M^n{\left(M^{*}\right)}^m$ and topological spin e^iπδ.

Fig. 2. Anyon collider of upstream modes.

It has counter-propagating edge channels, downstream charge modes (black arrows, label c) and upstream neutral modes (red arrows, label n). In this setup, the injection current I_A/B,inj at QPC_A/B results in the flow of upstream modes from QPC_A/B to QPC_C on Edge A/B. The locations of the charge sources (${\mathrm{S}}_{\mathrm{A}/\mathrm{B}},{\mathrm{S}}_{\mathrm{A}/\mathrm{B}}^{\prime }$) and detectors (${\mathrm{D}}_{\mathrm{A}/\mathrm{B}},{\mathrm{D}}_{\mathrm{A}/\mathrm{B}}^{\prime }$) are different from Fig. 1a.

Fig. 3. Monodromy M for non-Abelian anyons.

Two particle-hole pairs of ψ anyons are initially split from the vacuum (I). After the braiding, they fuse into the vacuum. The monodromy is the amplitude of this process. The red and blue loops correspond to anyons that tunnel at QPC_A/B and QPC_C, respectively [See the loops of the same colors in Fig. 1c]. Untying the topological link between the loops amounts to the monodromy M (or M^* depending on the direction of the loops).

Fig. 4. Dependence of Fano factor P_ref on I₋/I₊ for various anyons.

The Fano factors are shown for free fermions (gray dashed), Laughlin anyons at ν = 1/3 (black), anti-Pfaffian state at ν = 5/2 (APf, blue), particle-hole Pfaffian state at ν = 5/2 (PH-Pf, red), and anti-Read-Rezayi state at ν = 12/5 (ARR, purple). At any value of I₋/I₊, P_ref = −1 for the anti-Pfaffian state, P_ref = −π/4 for the particle-hole Pfaffian state, and $P_{\mathrm{ref}}=-5\sqrt{250-110\sqrt{5}}/4\pi \simeq -0.8$ for the anti-Read-Rezayi state. The behaviors of the non-Abelian anyons are distinguished from free fermions with P_ref = 0 and the Abelian anyons.