Effect of Human Behavior on the Evolution of Viral Strains During an Epidemic
- PMID: 36334172
- PMCID: PMC9638455
- DOI: 10.1007/s11538-022-01102-7
Effect of Human Behavior on the Evolution of Viral Strains During an Epidemic
Abstract
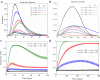
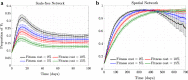
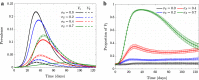
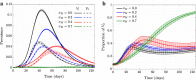
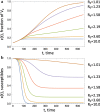
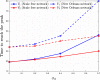
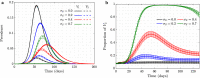
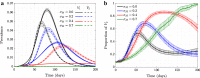
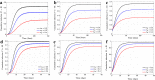
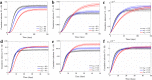
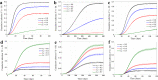
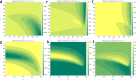
It is well known in the literature that human behavior can change as a reaction to disease observed in others, and that such behavioral changes can be an important factor in the spread of an epidemic. It has been noted that human behavioral traits in disease avoidance are under selection in the presence of infectious diseases. Here, we explore a complementary trend: the pathogen itself might experience a force of selection to become less "visible," or less "symptomatic," in the presence of such human behavioral trends. Using a stochastic SIR agent-based model, we investigated the co-evolution of two viral strains with cross-immunity, where the resident strain is symptomatic while the mutant strain is asymptomatic. We assumed that individuals exercised self-regulated social distancing (SD) behavior if one of their neighbors was infected with a symptomatic strain. We observed that the proportion of asymptomatic carriers increased over time with a stronger effect corresponding to higher levels of self-regulated SD. Adding mandated SD made the effect more significant, while the existence of a time-delay between the onset of infection and the change of behavior reduced the advantage of the asymptomatic strain. These results were consistent under random geometric networks, scale-free networks, and a synthetic network that represented the social behavior of the residents of New Orleans.
Keywords: Asymptomatic variant; Mandated social distancing; Network; Self-regulated social distancing; Symptomatic variant; Viral evolution.
© 2022. The Author(s), under exclusive licence to Society for Mathematical Biology.
Figures


Similar articles
-
Stochastic Models of Emerging Infectious Disease Transmission on Adaptive Random Networks.Comput Math Methods Med. 2017;2017:2403851. doi: 10.1155/2017/2403851. Epub 2017 Sep 17. Comput Math Methods Med. 2017. PMID: 29075314 Free PMC article.
-
A Network Epidemic Model with Preventive Rewiring: Comparative Analysis of the Initial Phase.Bull Math Biol. 2016 Dec;78(12):2427-2454. doi: 10.1007/s11538-016-0227-4. Epub 2016 Oct 31. Bull Math Biol. 2016. PMID: 27800576
-
Equilibria of an epidemic game with piecewise linear social distancing cost.Bull Math Biol. 2013 Oct;75(10):1961-84. doi: 10.1007/s11538-013-9879-5. Epub 2013 Aug 14. Bull Math Biol. 2013. PMID: 23943363 Free PMC article.
-
HIV competition dynamics over sexual networks: first comer advantage conserves founder effects.PLoS Comput Biol. 2015 Feb 5;11(2):e1004093. doi: 10.1371/journal.pcbi.1004093. eCollection 2015 Feb. PLoS Comput Biol. 2015. PMID: 25654450 Free PMC article.
-
Capturing the dynamics of pathogens with many strains.J Math Biol. 2016 Jan;72(1-2):1-24. doi: 10.1007/s00285-015-0873-4. Epub 2015 Mar 24. J Math Biol. 2016. PMID: 25800537 Free PMC article. Review.
Cited by
-
A modelling approach to characterise the interaction between behavioral response and epidemics: A study based on COVID-19.Infect Dis Model. 2024 Dec 26;10(2):477-492. doi: 10.1016/j.idm.2024.12.013. eCollection 2025 Jun. Infect Dis Model. 2024. PMID: 39845730 Free PMC article.
-
Activity-driven network modeling and control of the spread of two concurrent epidemic strains.Appl Netw Sci. 2022;7(1):66. doi: 10.1007/s41109-022-00507-6. Epub 2022 Sep 27. Appl Netw Sci. 2022. PMID: 36186912 Free PMC article.
-
Evolutionary safety of lethal mutagenesis driven by antiviral treatment.PLoS Biol. 2023 Aug 8;21(8):e3002214. doi: 10.1371/journal.pbio.3002214. eCollection 2023 Aug. PLoS Biol. 2023. PMID: 37552682 Free PMC article.
References
-
- Anderson RM, May RM. Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press; 1992.
-
- Ariful Kabir KM, Kuga K, Tanimoto J. Effect of information spreading to suppress the disease contagion on the epidemic vaccination game. Chaos Solitons Fractals. 2019;119:180–187.
-
- Arino J, Brauer F, van den Driessche P, Watmough J, Jianhong W. A final size relation for epidemic models. Math Biosci Eng. 2007;4(2):159. - PubMed

