Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jan:146:473-482.
doi: 10.1016/j.enganabound.2022.10.033. Epub 2022 Oct 31.

A mathematical model of coronavirus transmission by using the heuristic computing neural networks

Zulqurnain Sabir  1 , Adi Asmara  2 , Sanaullah Dehraj  3 , Muhammad Asif Zahoor Raja  4 , Gilder Cieza Altamirano  5 , Soheil Salahshour  6 , R Sadat  7 , Mohamed R Ali  8
Affiliations

A mathematical model of coronavirus transmission by using the heuristic computing neural networks

Zulqurnain Sabir et al. Eng Anal Bound Elem. 2023 Jan.

Abstract

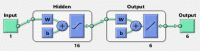
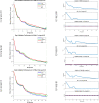
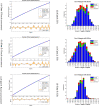
In this study, the nonlinear mathematical model of COVID-19 is investigated by stochastic solver using the scaled conjugate gradient neural networks (SCGNNs). The nonlinear mathematical model of COVID-19 is represented by coupled system of ordinary differential equations and is studied for three different cases of initial conditions with suitable parametric values. This model is studied subject to seven class of human population N(t) and individuals are categorized as: susceptible S(t), exposed E(t), quarantined Q(t), asymptotically diseased IA (t), symptomatic diseased IS (t) and finally the persons removed from COVID-19 and are denoted by R(t). The stochastic numerical computing SCGNNs approach will be used to examine the numerical performance of nonlinear mathematical model of COVID-19. The stochastic SCGNNs approach is based on three factors by using procedure of verification, sample statistics, testing and training. For this purpose, large portion of data is considered, i.e., 70%, 16%, 14% for training, testing and validation, respectively. The efficiency, reliability and authenticity of stochastic numerical SCGNNs approach are analysed graphically in terms of error histograms, mean square error, correlation, regression and finally further endorsed by graphical illustrations for absolute errors in the range of 10-05 to 10-07 for each scenario of the system model.

Keywords: COVID-19; Nonlinear; Numerical results; Quarantine; Runge-Kutta scheme; SCGNNs; Scaled conjugate gradient.

PubMed Disclaimer

Conflict of interest statement

All authors describe that there are no potential conflicts of interest.

Figures

Fig. 1
Fig. 1
Workflow illustrations of the SCGNNs to study the mathematical of COVID-19.
Fig. 2
Fig. 2
The organization of single neuron.
Fig. 3
Fig. 3
SCGNNs for nonlinear system with 16 neurons.
Fig. 4
Fig. 4
MSE and STs to investigate the proposed mathematical model of COVID-19.
Fig. 5
Fig. 5
Valuations and EHs to investigate the proposed mathematical model of COVID-19.
Fig. 6
Fig. 6
Comparison of the result to investigate proposed mathematical model of COVID-19.
Fig. 7
Fig. 7
AE to investigate proposed mathematical model of COVID-19.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Pinho S.T.R.D., Ferreira C.P., Esteva L., Barreto F.R., Morato e Silva V.C., Teixeira M.G.L. Modelling the dynamics of dengue real epidemics. Philos Trans R Soc A: Math, Phys Eng Sci, V. 2010;368(1933):5679–5693. - PubMed
    1. Umar Muhammad, Sabir Zulqurnain, Asif Zahoor Raja Muhammad, Baskonus Haci Mehmet, Yao Shao-Wen, Ilhan Esin. A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells. Res Phys. 2021;25
    1. Grassly N., Fraser C. Mathematical models of infectious disease transmission. Nat Rev, Microbiol. 2008;6(6):477–487. No. - PMC - PubMed
    1. Wu Y.C., Chen C.S., Chan Y.J. The outbreak of COVID-19: an overview. J Chin Med Assoc. 2020;83(3):217–220. No. - PMC - PubMed
    1. Dev S.M., Sengupta R. Indira Gandhi Institute of Development Research; Mumbai: 2020. Covid-19: Impact on the Indian economy.

LinkOut - more resources