A simple epidemic model for semi-closed community reveals the hidden outbreak risk in nursing homes, prisons, and residential universities
- PMID: 36339917
- PMCID: PMC9616437
- DOI: 10.1007/s40435-022-01068-3
A simple epidemic model for semi-closed community reveals the hidden outbreak risk in nursing homes, prisons, and residential universities
Abstract
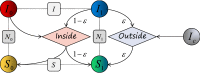
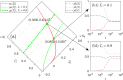
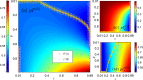
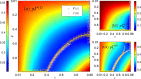
We develop a general SIS model to study the epidemic transmission in such semi-closed communities. The community population is divided into susceptible and infected in terms of the infection state, and concerning the physical structure of the crowd, they are classified into mobile and fixed individuals. The mobile individuals can be inside or outside the community, while the fixed individuals can be only inside the community. There are fixed infection sources outside the community, measuring the epidemic severity in society. We attribute the spreading to two reasons: (i) clustered infection among the community population and (ii) the epidemic in society spreading to the community population. We discuss the model in two cases. In the first case, the epidemic spreads in society, such that reasons (i) and (ii) work together. The results show that concerning fixed individuals (e.g. the elderly in nursing homes), a more closed community always promotes the infection. In the second case, there is no epidemic spreading in society, such that only reason (i) works. The results show that restricting all individuals to the community produces equivalent consequences as allowing them going outside the community. We should evenly distribute individuals inside and outside to form isolation. A counterexample is residential universities implementing closed management, where only students are restricted to campus. The model shows such management may lead to severe epidemics, and to prevent the epidemic outbreaks, students should have free access to being on or off campus.
Keywords: COVID-19; Closed management; Clustered infection; SIS model; Semi-closed community.
© The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature 2022, Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Conflict of interest statement
Conflict of interestNo Conflict of interest.
Figures

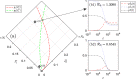
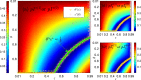
References
-
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc A. 1927;115(772):700–721.
LinkOut - more resources
Full Text Sources
