Ultrafast chirality: the road to efficient chiral measurements
- PMID: 36342056
- PMCID: PMC9673685
- DOI: 10.1039/d2cp01009g
Ultrafast chirality: the road to efficient chiral measurements
Abstract
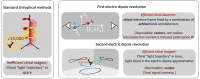
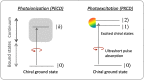
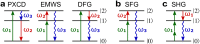
Today we are witnessing the electric-dipole revolution in chiral measurements. Here we reflect on its lessons and outcomes, such as the perspective on chiral measurements using the complementary principles of "chiral reagent" and "chiral observer", the hierarchy of scalar, vectorial and tensorial enantio-sensitive observables, the new properties of the chiro-optical response in the ultrafast and non-linear domains, and the geometrical magnetism associated with the chiral response in photoionization. The electric-dipole revolution is a landmark event. It has opened routes to extremely efficient enantio-discrimination with a family of new methods. These methods are governed by the same principles but work in vastly different regimes - from microwaves to optical light; they address all molecular degrees of freedom - electronic, vibrational and rotational, and use flexible detection schemes, i.e. detecting photons or electrons, making them applicable to different chiral phases, from gases to liquids to amorphous solids. The electric-dipole revolution has also enabled enantio-sensitive manipulation of chiral molecules with light. This manipulation includes exciting and controlling ultrafast helical currents in vibronic states of chiral molecules, enantio-sensitive control of populations in electronic, vibronic and rotational molecular states, and opens the way to efficient enantio-separation and enantio-sensitive trapping of chiral molecules. The word "perspective" has two meanings: an "outlook" and a "point of view". In this perspective article, we have tried to cover both meanings.
Conflict of interest statement
There are no conflicts to declare.
Figures









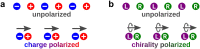

References
-
- Wade L. G., Chirality in Drug Research, Prentice Hall, 2003
Publication types
LinkOut - more resources
Full Text Sources

