Regression models using the LINEX loss to predict lower bounds for the number of points for approximating planar contour shapes
- PMID: 36353295
- PMCID: PMC9639494
- DOI: 10.1080/02664763.2021.1986685
Regression models using the LINEX loss to predict lower bounds for the number of points for approximating planar contour shapes
Abstract
Researchers in statistical shape analysis often analyze outlines of objects. Even though these contours are infinite-dimensional in theory, they must be discretized in practice. When discretizing, it is important to reduce the number of sampling points considerably to reduce computational costs, but to not use too few points so as to result in too much approximation error. Unfortunately, determining the minimum number of points needed to achieve sufficiently approximate the contours is computationally expensive. In this paper, we fit regression models to predict these lower bounds using characteristics of the contours that are computationally cheap as predictor variables. However, least squares regression is inadequate for this task because it treats overestimation and underestimation equally, but underestimation of lower bounds is far more serious. Instead, to fit the models, we use the LINEX loss function, which allows us to penalize underestimation at an exponential rate while penalizing overestimation only linearly. We present a novel approach to select the shape parameter of the loss function and tools for analyzing how well the model fits the data. Through validation methods, we show that the LINEX models work well for reducing the underestimation for the lower bounds.
Keywords: 62H35; 62J05; 62J20; LINEX loss function; Linear regression; lower bound prediction; planar contours; shape analysis.
© 2021 Informa UK Limited, trading as Taylor & Francis Group.
Conflict of interest statement
No potential conflict of interest was reported by the author(s).
Figures





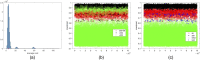


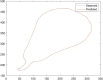
References
-
- Akdeniz F., New biased estimators under the LINEX loss function, Statist. Papers 45 (2004), pp. 175–190.
-
- Cain M. and Janssen C., Real estate price prediction under asymmetric loss, Ann. Inst. Stat. Math. 47 (1995), pp. 401–414.
-
- Chang Y.C. and Hung W.L., LINEX loss functions with applications to determining the optimum process parameters, Qual. Quant. 41 (2007), pp. 291–301.
-
- Chaturvedi A., Bhatti M.I., and Kumar K., Bayesian analysis of disturbances variance in the linear regression model under asymmetric loss functions, Appl. Math. Comput. 114 (2000), pp. 149–153.
-
- Dryden I.L. and Mardia K.V., Statistical Shape Analysis: With Applications in R, Vol. 995, John Wiley & Sons, Chichester, 2016.
LinkOut - more resources
Full Text Sources
Other Literature Sources
