Chiral Dirac-like fermion in spin-orbit-free antiferromagnetic semimetals

Abstract

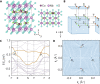
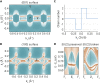
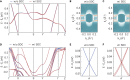
Dirac semimetal is a phase of matter whose elementary excitation is described by the relativistic Dirac equation. In the limit of zero mass, its parity-time symmetry enforces the Dirac fermion in the momentum space, which is composed of two Weyl fermions with opposite chirality, to be non-chiral. Inspired by the flavor symmetry in particle physics, we theoretically propose a massless Dirac-like equation yet linking two Weyl fields with the identical chirality by assuming $\mathrm{SU}\left(2\right)$ isospin symmetry, independent of the space-time rotation exchanging the two fields. Dramatically, such symmetry is hidden in certain solid-state spin-1/2 systems with negligible spin-orbit coupling, where the spin degree of freedom is decoupled with the lattice. Therefore, the existence of the corresponding quasiparticle, dubbed as flavor Weyl fermion, cannot be explained by the conventional (magnetic) space group framework. The 4-fold degenerate flavor Weyl fermion manifests linear dispersion and a Chern number of $\pm$ 2, leading to a robust network of topologically protected Fermi arcs throughout the Brillouin zone. For material realization, we show that the transition-metal chalcogenide CoNb₃S₆ with experimentally confirmed collinear antiferromagnetic order is ideal for flavor Weyl semimetal under the approximation of vanishing spin-orbit coupling. Our work reveals a counterpart of the flavor symmetry in magnetic electronic systems, leading to further possibilities of emergent phenomena in quantum materials.

Keywords: Weyl fermion; antiferromagnet; isospin symmetry; spin group; topological semimetal.

Graphical abstract

Figure 1

Schematics of the Dirac semimetal (DSM) and flavor Weyl semimetal (flavor WSM) (A) A Dirac point can be viewed as the superposition of two Weyl points with opposite chirality in a DSM. Such superposition is generally obtained by the space-time $PT$ symmetry. (B) The surface states of the DSM are adiabatically connected to topologically trivial surface states. The green points denote the Dirac points. (C) A flavor WSM hosts 4-fold degenerate points composed of two Weyl points with identical chirality, protected by a hidden $SU\left(2\right)$ symmetry group (analogous to the isospin symmetry in particle physics). (D) The surface states of flavor WSM are robust owing to the protection of chiral charges. The surface states on the surfaces that preserve the $SU\left(2\right)$ symmetry are 2-fold degenerate connecting two flavor Weyl points with opposite chirality. However, the surface states on the surfaces with a broken $SU\left(2\right)$ symmetry group split into two spin-polarized branches, resembling conventional topological insulators or semimetals.

Figure 2

Hidden $\mathit{SU}\left(2\right)$ symmetry in antiferromagnetic materials (A) The magnetic lattice with collinear antiferromagnetic order allows spin-group symmetry operations, $\left\{U_x\left(\pi \right)|\left|E\right|{\mathit{\tau }}_{1/2}\right\}\text{ and }\left\{U_z\left(\theta \right)|\left|E\right|0\right\}$ without spin-orbit coupling, leading to two degenerate Weyl cones with the basis $\left\{|A,\uparrow ⟩,|B,\uparrow ⟩\right\}$ and $\left\{|B,\downarrow ⟩,|A,\downarrow ⟩\right\}$ and an $SU\left(2\right)$ symmetry group $exp\left(-i\theta \mathit{n}\cdot \mathit{\rho }\right)$ (see the main text). (B) Bloch sphere of the $SU\left(2\right)$ symmetry group, transforming the basis of a Weyl cone $\left\{|A,\uparrow ⟩,|B,\uparrow ⟩\right\}$ (blue arrow) to any linear combinations (up to a phase factor) $\left\{\alpha \left|A,\uparrow ⟩+\beta \right|B,\downarrow ⟩,\alpha |B,\uparrow ⟩+\beta |A,\downarrow ⟩\right\}$, and transforming $\left\{|B,\downarrow ⟩,|A,\downarrow ⟩\right\}$ (red arrow) to an orthogonal one $\left\{-{\beta }^{\ast }\left|A,\uparrow ⟩+{\alpha }^{\ast }\right|B,\downarrow ⟩,-{\beta }^{\ast }|B,\uparrow ⟩+{\alpha }^{\ast }|A,\downarrow ⟩\right\}$. The basis transformation under the rotation axis (gray line) $\mathit{n}=(cos\left(\omega \right),sin\left(\omega \right),0)$ and rotation angle $\theta$ are also shown. The mixing coefficients are $\alpha =cos\left[\theta /2\right]$ and $\beta =-isin\left[\theta /2\right]e^{-i\omega }$.

Figure 3

Crystal and bulk electronic properties of CoNb₃S₆ (A) The crystal structure of CoNb₃S₆. (B) Bulk and surface Brillouin zones of CoNb₃S₆. (C) The band structure of CoNb₃S₆ without spin-orbit coupling. There are two flavor Weyl points at ∼0.7 eV above the Fermi level, $N_1$ and $P_1$, and another two flavor Weyl points, $N_2$ and $P_2$ (not shown), that are connected to $N_1$ and $P_1$ through 2-fold rotation. (D) Distribution of in-plane components of thetrace of Berry curvature tensor on $k_z=0$ plane, where $N_1$/ $N_2$ and $P_1$/ $P_2$ denote the source and sink, respectively.

Figure 4

Protected topological surface states of flavor WSM CoNb₃S₆ (A and B) Iso-energy surface states connect electron pockets and hole pockets, separately enclosing flavor Weyl points with opposite chirality on (001) and (100) surfaces of CoNb₃S₆. (C) The transition of Chern number defined on 2D slices in the Brillouin zone perpendicular to the y axis as a function of momentum $k_y$. (D) Chiral edge states of the 2D slice ($k_y$ = 0.1 ($2\pi /b$)) with Chern number of 2. Doubly degenerate edge bands are found in $SU\left(2\right)$-preserved edge, while spin-polarized nondegenerate edge bands are found in $SU\left(2\right)$-broken edge. The notations are defined as ${\overline{\text{Γ}}}_1=\overline{\text{Γ}}+\overline{P}$${\overline{X}}_1=\overline{X}+\overline{P}$, ${\overline{\text{Γ}}}_2=\overline{\text{Γ}}+\overline{P}$, and ${\overline{Z}}_2=\overline{Z}+\overline{P}$, where $\overline{P}=\frac{1}{5}\left(\overline{Y}-\overline{\text{Γ}}\right)$.

Figure 5

Effects of spin-orbit coupling on energy bands (A) Band structure around the energies of $N_1$ and $P_1$. (B and C) Iso-energy topological surface states without SOC (B) and with SOC (C). The energy is set between those of $N_1$ and $P_1$. (D) Band structure around the Fermi level. (E and F) Zoom-in bands of a flavor Weyl point without SOC (E) and with SOC (F). The coordinate of points labeled are $A=\left(0.5,0.2572,0\right),A^{\prime }=\left(0.5,0.2575,0\right),\delta =\left(0.05,0,0\right)$.