SpiDec: Computing binodals and interfacial tension of biomolecular condensates from simulations of spinodal decomposition
- PMID: 36353733
- PMCID: PMC9637972
- DOI: 10.3389/fmolb.2022.1021939
SpiDec: Computing binodals and interfacial tension of biomolecular condensates from simulations of spinodal decomposition
Abstract
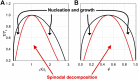
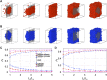
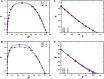
Phase separation of intrinsically disordered proteins (IDPs) is a phenomenon associated with many essential cellular processes, but a robust method to compute the binodal from molecular dynamics simulations of IDPs modeled at the all-atom level in explicit solvent is still elusive, due to the difficulty in preparing a suitable initial dense configuration and in achieving phase equilibration. Here we present SpiDec as such a method, based on spontaneous phase separation via spinodal decomposition that produces a dense slab when the system is initiated at a homogeneous, low density. After illustrating the method on four model systems, we apply SpiDec to a tetrapeptide modeled at the all-atom level and solvated in TIP3P water. The concentrations in the dense and dilute phases agree qualitatively with experimental results and point to binodals as a sensitive property for force-field parameterization. SpiDec may prove useful for the accurate determination of the phase equilibrium of IDPs.
Keywords: binodal; biomolecular condensates; interfacial tension; phase equilibrium; phase separation; spinodal decomposition.
Copyright © 2022 Mazarakos, Prasad and Zhou.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures



Similar articles
-
Calculating Binodals and Interfacial Tension of Phase-Separated Condensates from Molecular Simulations with Finite-Size Corrections.Methods Mol Biol. 2023;2563:1-35. doi: 10.1007/978-1-0716-2663-4_1. Methods Mol Biol. 2023. PMID: 36227466 Free PMC article.
-
FIREBALL: A tool to fit protein phase diagrams based on mean-field theories for polymer solutions.bioRxiv [Preprint]. 2023 Mar 22:2023.03.19.533322. doi: 10.1101/2023.03.19.533322. bioRxiv. 2023. Update in: Biophys J. 2023 Jun 20;122(12):2396-2403. doi: 10.1016/j.bpj.2023.05.007. PMID: 36993371 Free PMC article. Updated. Preprint.
-
FIREBALL: A tool to fit protein phase diagrams based on mean-field theories for polymer solutions.Biophys J. 2023 Jun 20;122(12):2396-2403. doi: 10.1016/j.bpj.2023.05.007. Epub 2023 May 8. Biophys J. 2023. PMID: 37161095 Free PMC article.
-
Making the Case for Disordered Proteins and Biomolecular Condensates in Bacteria.Trends Biochem Sci. 2020 Aug;45(8):668-680. doi: 10.1016/j.tibs.2020.04.011. Epub 2020 May 23. Trends Biochem Sci. 2020. PMID: 32456986 Review.
-
Conformational Dynamics of Intrinsically Disordered Proteins Regulate Biomolecular Condensate Chemistry.Chem Rev. 2022 Mar 23;122(6):6719-6748. doi: 10.1021/acs.chemrev.1c00774. Epub 2022 Feb 18. Chem Rev. 2022. PMID: 35179885 Free PMC article. Review.
Cited by
-
Amino acid-dependent phase equilibrium and material properties of tetrapeptide condensates.Cell Rep Phys Sci. 2024 Oct 16;5(10):102218. doi: 10.1016/j.xcrp.2024.102218. Epub 2024 Sep 23. Cell Rep Phys Sci. 2024. PMID: 39513041 Free PMC article.
-
Fundamental Aspects of Phase-Separated Biomolecular Condensates.Chem Rev. 2024 Jul 10;124(13):8550-8595. doi: 10.1021/acs.chemrev.4c00138. Epub 2024 Jun 17. Chem Rev. 2024. PMID: 38885177 Free PMC article. Review.
-
Amino Acid-Dependent Material Properties of Tetrapeptide Condensates.bioRxiv [Preprint]. 2024 May 15:2024.05.14.594233. doi: 10.1101/2024.05.14.594233. bioRxiv. 2024. Update in: Cell Rep Phys Sci. 2024 Oct 16;5(10):102218. doi: 10.1016/j.xcrp.2024.102218. PMID: 38798623 Free PMC article. Updated. Preprint.
-
Phase separation of multicomponent peptide mixtures into dehydrated clusters with hydrophilic cores.Biophys J. 2024 Feb 6;123(3):349-360. doi: 10.1016/j.bpj.2023.12.027. Epub 2024 Jan 1. Biophys J. 2024. PMID: 38163950 Free PMC article.
-
A computational pipeline for image-based statistical analysis of biomolecular condensates dynamics using morphological descriptors.Sci Rep. 2025 Jul 29;15(1):27560. doi: 10.1038/s41598-025-09148-y. Sci Rep. 2025. PMID: 40730560 Free PMC article.
References
-
- Berendsen H. J. C., Postma J. P. M., Gunsteren W. F. v., DiNola A., Haak J. R. (1984). Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690. 10.1063/1.448118 - DOI
-
- Binder K., Block B. J., Virnau P., Tröster A. (2012). Beyond the van der Waals loop: What can Be learned from simulating Lennard-Jones fluids inside the region of phase coexistence. Am. J. Phys. 80, 1099–1109. 10.1119/1.4754020 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

