Model-Based Tracking of Fruit Flies in Free Flight
- PMID: 36354842
- PMCID: PMC9692569
- DOI: 10.3390/insects13111018
Model-Based Tracking of Fruit Flies in Free Flight
Abstract
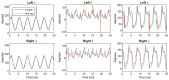
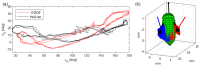
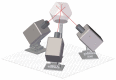
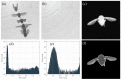
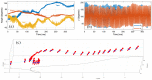
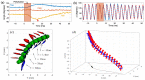
Insect flight is a complex interdisciplinary phenomenon. Understanding its multiple aspects, such as flight control, sensory integration, physiology and genetics, often requires the analysis of large amounts of free flight kinematic data. Yet, one of the main bottlenecks in this field is automatically and accurately extracting such data from multi-view videos. Here, we present a model-based method for the pose estimation of free-flying fruit flies from multi-view high-speed videos. To obtain a faithful representation of the fly with minimum free parameters, our method uses a 3D model that includes two new aspects of wing deformation: A non-fixed wing hinge and a twisting wing surface. The method is demonstrated for free and perturbed flight. Our method does not use prior assumptions on the kinematics apart from the continuity of the wing pitch angle. Hence, this method can be readily adjusted for other insect species.
Keywords: drosophila; insect flight; pose estimation; tracking.
Conflict of interest statement
The authors declare no conflict of interest.
Figures




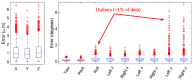
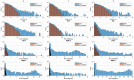
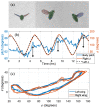
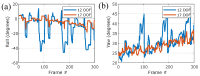
References
-
- Dudley R. The Biomechanics of Insect Flight: Form, Function, Evolution. Princeton University Press; Princeton, NJ, USA: 2002.
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Molecular Biology Databases

