Perspective on the Current State-of-the-Art of Quantum Computing for Drug Discovery Applications
- PMID: 36355616
- PMCID: PMC9753588
- DOI: 10.1021/acs.jctc.2c00574
Perspective on the Current State-of-the-Art of Quantum Computing for Drug Discovery Applications
Abstract
Computational chemistry is an essential tool in the pharmaceutical industry. Quantum computing is a fast evolving technology that promises to completely shift the computational capabilities in many areas of chemical research by bringing into reach currently impossible calculations. This perspective illustrates the near-future applicability of quantum computation of molecules to pharmaceutical problems. We briefly summarize and compare the scaling properties of state-of-the-art quantum algorithms and provide novel estimates of the quantum computational cost of simulating progressively larger embedding regions of a pharmaceutically relevant covalent protein-drug complex involving the drug Ibrutinib. Carrying out these calculations requires an error-corrected quantum architecture that we describe. Our estimates showcase that recent developments on quantum phase estimation algorithms have dramatically reduced the quantum resources needed to run fully quantum calculations in active spaces of around 50 orbitals and electrons, from estimated over 1000 years using the Trotterization approach to just a few days with sparse qubitization, painting a picture of fast and exciting progress in this nascent field.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
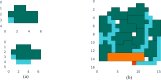

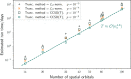
 . Note that, for larger molecules, ϵ0 for small values of τ appear to deviate from the quadratic
behavior. We attribute this to numerical error and exclude these values
from the fits. In the second step (right), we plot a1 for each molecule and fit a1 = a(nq)b, obtaining the parameters of the empirical law in eq 38: a =
1.51 ± 0.84; b = −4.66 ± 0.27.
. Note that, for larger molecules, ϵ0 for small values of τ appear to deviate from the quadratic
behavior. We attribute this to numerical error and exclude these values
from the fits. In the second step (right), we plot a1 for each molecule and fit a1 = a(nq)b, obtaining the parameters of the empirical law in eq 38: a =
1.51 ± 0.84; b = −4.66 ± 0.27.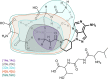


References
-
- Lam Y.-h.; Abramov Y.; Ananthula R. S.; Elward J. M.; Hilden L. R.; Nilsson Lill S. O.; Norrby P.-O.; Ramirez A.; Sherer E. C.; Mustakis J.; Tanoury G. J. Applications of Quantum Chemistry in Pharmaceutical Process Current State and Opportunities. Org. Process Res. Dev. 2020, 24, 1496–1507. 10.1021/acs.oprd.0c00222. - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

