Domain Decomposition Spectral Method Applied to Modal Method: Direct and Inverse Spectral Transforms
- PMID: 36365826
- PMCID: PMC9657735
- DOI: 10.3390/s22218131
Domain Decomposition Spectral Method Applied to Modal Method: Direct and Inverse Spectral Transforms
Abstract
We introduce a Domain Decomposition Spectral Method (DDSM) as a solution for Maxwell's equations in the frequency domain. It will be illustrated in the framework of the Aperiodic Fourier Modal Method (AFMM). This method may be applied to compute the electromagnetic field diffracted by a large-scale surface under any kind of incident excitation. In the proposed approach, a large-size surface is decomposed into square sub-cells, and a projector, linking the set of eigenvectors of the large-scale problem to those of the small-size sub-cells, is defined. This projector allows one to associate univocally the spectrum of any electromagnetic field of a problem stated on the large-size domain with its footprint on the small-scale problem eigenfunctions. This approach is suitable for parallel computing, since the spectrum of the electromagnetic field is computed on each sub-cell independently from the others. In order to demonstrate the method's ability, to simulate both near and far fields of a full three-dimensional (3D) structure, we apply it to design large area diffractive metalenses with a conventional personal computer.
Keywords: metalens; metasurfaces.
Conflict of interest statement
The author declares there are no conflict of interest.
Figures




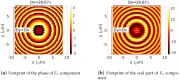
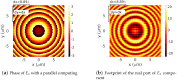




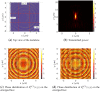

References
-
- Gander M.J., Zhang H. A class of iterative solvers for the Helmholtz equation: Factorizations, sweeping preconditioners, source transfer, single layer potentials, polarized traces, and optimized Schwarz methods. SIAM Rev. 2019;61:1–76. doi: 10.1137/16M109781X. - DOI
-
- Zepeda-Núñez L., Demanet L. Nested domain decomposition with polarized traces for the 2d Helmholtz equation. SIAM J. Sci. Comput. 2018;40:B942–B981.
-
- Stolk C.C. A rapidly converging domain decomposition method for the Helmholtz equation. J. Comput. Phys. 2013;241:240–252. doi: 10.1016/j.jcp.2013.01.039. - DOI
-
- Chen Z., Xiang X. A source transfer domain decomposition method for Helmholtz equations in unbounded domain. SIAM J. Numer. Anal. 2013;51:2331–2356. doi: 10.1137/130917144. - DOI
-
- Vouvakis M., Zhao K., Lee J.-F. Modeling large almost periodic structures using a non-overlapping domain decomposition method; Proceedings of the IEEE Antennas and Propagation Society Symposium; Monterey, CA, USA. 20–25 June 2004; pp. 343–346.
LinkOut - more resources
Full Text Sources

