New Insights into the Estimation of Reproduction Numbers during an Epidemic
- PMID: 36366299
- PMCID: PMC9694736
- DOI: 10.3390/vaccines10111788
New Insights into the Estimation of Reproduction Numbers during an Epidemic
Abstract
In this paper, we deal with the problem of estimating the reproduction number Rt during an epidemic, as it represents one of the most used indicators to study and control this phenomenon. In particular, we focus on two issues. First, to estimate Rt, we consider the use of positive test case data as an alternative to the first symptoms data, which are typically used. We both theoretically and empirically study the relationship between the two approaches. Second, we modify a method for estimating Rt during an epidemic that is widely used by public institutions in several countries worldwide. Our procedure is not affected by the problems deriving from the hypothesis of Rt local constancy, which is assumed in the standard approach. We illustrate the results obtained by applying the proposed methodologies to real and simulated SARS-CoV-2 datasets. In both cases, we also apply some specific methods to reduce systematic and random errors affecting the data. Our results show that the Rt during an epidemic can be estimated by using the positive test data, and that our estimator outperforms the standard estimator that makes use of the first symptoms data. It is hoped that the techniques proposed here could help in the study and control of epidemics, particularly the current SARS-CoV-2 pandemic.
Keywords: SARS-CoV-2; epidemic evolution; estimation techniques; mathematical analysis; reproduction number.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

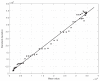

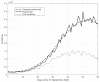



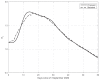






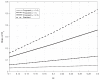
References
-
- Cauchemez S., Fraser C., Van Kerkhove M.D., Donnelly C.A., Riley S., Rambaut A., Enouf V., van der Werf S., Ferguson N.M. Middle East respiratory syndrome coronavirus: Quantification of the extent of the epidemic, surveillance biases, and transmissibility. Lancet Infect. Dis. 2014;14:50–56. doi: 10.1016/S1473-3099(13)70304-9. - DOI - PMC - PubMed
-
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A. 1927;115:700–721.
LinkOut - more resources
Full Text Sources
Miscellaneous

