Role of ambient temperature in modulation of behavior of vanadium dioxide volatile memristors and oscillators for neuromorphic applications

Abstract

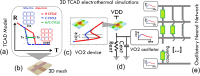
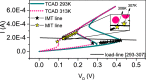
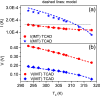
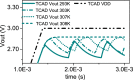
Volatile memristors are versatile devices whose operating mechanism is based on an abrupt and volatile change of resistivity. This switching between high and low resistance states is at the base of cutting edge technological implementations such as neural/synaptic devices or random number generators. A detailed understanding of this operating mechanisms is essential prerequisite to exploit the full potentiality of volatile memristors. In this respect, multi-physics device simulations provide a powerful tool to single out material properties and device features that are the keys to achieve desired behaviors. In this paper, we perform 3D electrothermal simulations of volatile memristors based on vanadium dioxide (VO[Formula: see text]) to accurately investigate the interplay among Joule effect, heat dissipation and the external temperature [Formula: see text] over their resistive switching mechanism. In particular, we extract from our simulations a simplified model for the effect of [Formula: see text] over the negative differential resistance (NDR) region of such devices. The NDR of VO[Formula: see text] devices is pivotal for building VO[Formula: see text] oscillators, which have been recently shown to be essential elements of oscillatory neural networks (ONNs). ONNs are innovative neuromorphic circuits that harness oscillators' phases to compute. Our simulations quantify the impact of [Formula: see text] over figures of merit of VO[Formula: see text] oscillator, such as frequency, voltage amplitude and average power per cycle. Our findings shed light over the interlinked thermal and electrical behavior of VO[Formula: see text] volatile memristors and oscillators, and provide a roadmap for the development of ONN technology.

Figure 1

Example of possible ONN application for image recognition tasks. (a) Input image. (b) Initialization of ONN circuit. Each pixel of input image is mapped as oscillator’s phase $\mathrm{\Delta }{\mathrm{\Phi }}_{\mathrm{in},\mathrm{j}}$ by delaying of $\mathrm{\Delta }{t}_{\mathrm{in},\mathrm{j}}$ the biasing $V_{\mathrm{DD},\mathrm{j}}$ compared to the reference (bottom-most) oscillator. The computation begins at coupling of all the oscillators (c), where the simplest coupling elements are resistances $R_{\mathrm{C},\mathrm{i},\mathrm{j}}$ (green blocks). (d) The oscillators synchronize in a stable in-phase ($\mathrm{\Delta }{\mathrm{\Phi }}_{\mathrm{out},\mathrm{j}}=0^{\circ }$) or out-of-phase ($\mathrm{\Delta }{\mathrm{\Phi }}_{\mathrm{out},\mathrm{j}}\ne 0^{\circ }$) state. The phase of each oscillator is mapped back as pixel (gray scale) color to yield the (e) output image.

Figure 2

(a) Temperature-triggered resistive switching of VO${}_2$ volatile memristor. (b) 3D mesh of VO${}_2$ CB device. (c) TCAD simulated I–$V_{\mathrm{D}}$ characteristics. The associated NDR region has been highlighted. (d) Scheme of VO${}_2$ oscillator circuit. Self-oscillatory electrical behavior is associated to a suitable choice of the load-line. (e) ONN.

Figure 3

Simulated I–$V_D$ at external temperature of $T_0=293$ K (solid dark cyan line) and $T_0=313$ K (pink dotted line). The IMT/MIT points for $T_0$ ranging from 293 K (the rightmost ones) to 313 K (the leftmost ones) are shown as black (IMT) and yellow (MIT) starred lines, respectively. The black line is the load line valid for the temperature interval [293–307] K. The inset shows the MIT points for $T_0=307$ K (on the right) and $T_0=308$ K (on the left). It is evident that the MIT point for $T_0=307$ K is above the load-line, while the MIT point for $T_0=308$ K is below it.

Figure 4

(a) Local temperatures probed in the geometrical center of the device as extracted by TCAD simulations (dark cyan solid lines) for $T_0$ equal to 293 and 313 K. We achieve a very good agreement with temperatures calculated after Eq. (4) for $\alpha =5.15\times {10}^5$ K$/$W (pink dashed lines). (b) $\mathrm{\Delta }{T}_{\mathrm{IMT}}$ (red triangles) and $\mathrm{\Delta }{T}_{\mathrm{MIT}}$ (blue triangles) as determined by TCAD simulations for different $T_0$. The dotted lines are the correspondent fits by 2nd order polynomials.

Figure 5

(a) $I_{\mathrm{IMT}}$ (red pentagons), $I_{\mathrm{MIT}}$ (blue stars) and (b) $V_{\mathrm{IMT}}$ (red circles), $V_{\mathrm{MIT}}$ (blue diamonds) as derived from TCAD simulations. The dashed lines are the currents and voltages as calculated from the proposed model. In (a), the black solid line is drawn parallel to $T_0$ axis. It intersects the $I_{\mathrm{IMT}}$ line at $T_0=293$ K, and the $I_{\mathrm{MIT}}$ line at about $T_0=312$ K.

Figure 6

TCAD simulated voltage oscillations for $V_{\mathrm{DD}}=3$ V, $R_{\mathrm{ext}}=15$ k$\mathrm{\Omega }$ and $C_{\mathrm{ext}}=1.5\times {10}^{-7}$ F, at external temperature of $T_0=293$ K (solid line), $T_0=303$ K (dash-dotted line), $T_0=307$ K (dotted line) and $T_0=308$ K (dashed line).

Figure 7

(a) Frequency of voltage oscillations vs the external temperature for $C_{\mathrm{ext}}=150$ nF (dark cyan triangles) and $C_{\mathrm{ext}}=40$ nF (pink stars). The curves obtained by the model of capacitor charging and discharging (pink dashed and dark cyan solid lines) are also plotted. (b) TCAD simulated periods of charging ${\tau }_{\mathrm{ch}}$ (downward triangles) and discharging ${\tau }_{\mathrm{dis}}$ (upward triangles) for $C_{\mathrm{ext}}=150$ nF. The dotted and dashed lines are the curves for ${\tau }_{\mathrm{ch}}$, ${\tau }_{\mathrm{dis}}$ by applying the circuit equations.