The numerical solution of a mathematical model of the Covid-19 pandemic utilizing a meshless local discrete Galerkin method

Abstract

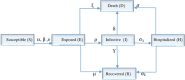
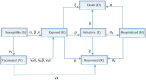
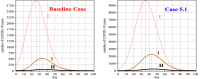
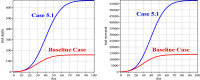
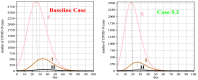
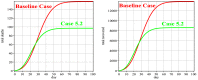
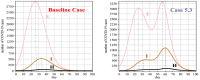
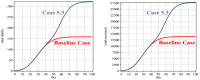
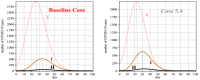
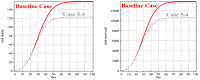
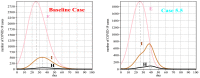
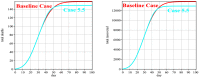
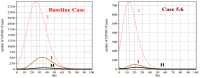
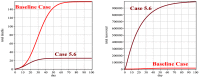
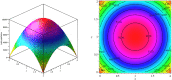
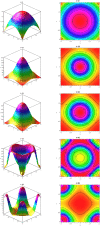
It was in early December 2019 that the terrible news of the outbreak of new coronavirus disease (Covid-19) was reported by the world media, which appeared in Wuhan, China, and is rapidly spreading to other parts of China and several overseas countries. In the field of infectious diseases, modeling, evaluating, and predicting the rate of disease transmission are very important for epidemic prevention and control. Several preliminary mathematical models for Covid-19 are formulated by various international study groups. In this article, the SEIHR(D) compartmental model is proposed to study this epidemic and the factors affecting it, including vaccination. The proposed model can be used to compute the trajectory of the spread of the disease in different countries. Most importantly, it can be used to predict the impact of different inhibition strategies on the development of Covid-19. A computational approach is applied to solve the offered model utilizing the Galerkin method based on the moving least squares approximation constructed on a set of scattered points as a locally weighted least square polynomial fitting. As the method does not need any background meshes, its algorithm can be easily implemented on computers. Finally, illustrative examples clearly show the reliability and efficiency of the new technique and the obtained results are in good agreement with the known facts about the Covid-19 pandemic.

Keywords: Covid-19 pandemic; Galerkin method; Integral equation; Meshless method; Moving least squares; SEIHR(D)-compartment model.

Fig. 1

The proposed compartmental epidemic model

Fig. 2

The proposed compartmental epidemic model with vaccination effect

Fig. 3

Graphs of E(t), I(t) and H(t) for Case 1 in comparison with the baseline case

Fig. 4

Number of people deaths and recovery for Case 1 in comparison with the baseline case

Fig. 5

Graphs of E(t), I(t) and H(t) for Case 2 in comparison with the baseline case

Fig. 6

Number of people deaths and recovery for Case 2 in comparison with the baseline case

Fig. 7

Graphs of E(t), I(t) and H(t) for Case 3 in comparison with the baseline case

Fig. 8

Number of people deaths and recovery for Case 3 in comparison with the baseline case

Fig. 9

Graphs of E(t), I(t) and H(t) for Case 4 in comparison with the baseline case

Fig. 10

Number of people deaths and recovery for Case 4 in comparison with the baseline case

Fig. 11

Graphs of E(t), I(t) and H(t) for Case 5 in comparison with the baseline case

Fig. 12

Number of people deaths and recovery for Case 5 in comparison with the baseline case

Fig. 13

Graphs of E(t), I(t) and H(t) for Case 6 in comparison with the baseline case

Fig. 14

Number of people deaths and recovery for Case 6 in comparison with the baseline case

Fig. 15

Simulation of the total population in the target domain

Fig. 16

Simulating the target domain for the exposed population

Fig. 17

Simulation of deaths in the target domain up to time $t=80$ (total)