Dispersion of free-falling saliva droplets by two-dimensional vortical flows

Abstract

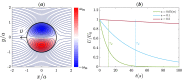
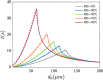
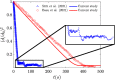
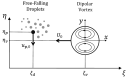
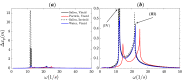
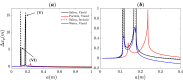
Abstract: The dispersion of respiratory saliva droplets by indoor wake structures may enhance the transmission of various infectious diseases, as the wake spreads virus-laden droplets across the room. Thus, this study analyzes the interaction between vortical wake structures and exhaled multi-component saliva droplets. A self-propelling analytically described dipolar vortex is chosen as a model wake flow, passing through a cloud of micron-sized evaporating saliva droplets. The droplets' spatial location, velocity, diameter, and temperature are traced, coupled to their local flow field. For the first time, the wake structure decay is incorporated and analyzed, which is proved essential for accurately predicting the settling distances of the dispersed droplets. The model also considers the nonvolatile saliva components, adequately capturing the essence of droplet-aerosol transition and predicting the equilibrium diameter of the residual aerosols. Our analytic model reveals non-intuitive interactions between wake flows, droplet relaxation time, gravity, and transport phenomena. We reveal that given the right conditions, a virus-laden saliva droplet might translate to distances two orders of magnitude larger than the carrier-flow characteristic size. Moreover, accounting for the nonvolatile contents inside the droplet may lead to fundamentally different dispersion and settling behavior compared to non-evaporating particles or pure water droplets. Ergo, we suggest that the implementation of more complex evaporation models might be critical in high-fidelity simulations aspiring to assess the spread of airborne respiratory droplets.

Keywords: Droplet evaporation; Lamb–Chaplygin dipole; Wake flows.

Fig. 1

a Lamb–Chaplygin vortex dipole streamlines and vorticity field $\omega (\overline{x},\overline{y})$, illustrated at the normalized frame of reference fixed to the dipole center. b Comparison of the dipole’s rate of viscid decay for different core sizes, represented by the ratio between the translation velocity and its initial value. vertical dotted lines demonstrate the characteristic decay times for each core size

Fig. 2

Airborne lifetime of a $T_{d,0}=306$ K water droplet free-falling in quiescent air ($T_{\infty }=291$ K) and various relative humidities, as a function of its initial diameter. Solid lines represent the current study predicaments, and dashed lines are modeling results of Xie et al. [8]

Fig. 3

Comparison of evaporation rates of levitating saliva droplet measured by Stiti et al. [41] (blue triangles), Basu et al. [42] (red circles), and the numerical solution of the current study (solid lines) (color figure online)

Fig. 4

Flow-particle configuration illustrated with respect to the stationary frame of reference $(\xi ,\eta )$. Droplets, initially placed at $({\xi }_p,{\eta }_p)$, free fall due to gravity $\overline{g}$. A vortex dipole flow-field initially placed at $({\xi }_v,{\eta }_v)$, is self-propelling toward the free-falling droplets at a velocity $U_0$

Fig. 5

Instantaneous snapshots of the dispersion caused by a vortex of initial maximal intensity ${\omega }_{m,0}=10{\text{s}}^{-}1$, radius of $a=0.1$ m, and initial propagation velocity $U_0\approx 0.1$ m/s passing through a dilute cloud of $d_0=65$ $\mathrm{\mu }\text{m}$ saliva droplets. The dashed line represents the vortex core, moving from right to left. Subplots (a–e) illustrate the cloud dispersion at different times. Both axes are normalized using the vortex radius a

Fig. 6

Droplet spatial density as function of the normalized horizontal location at time instances $t_a=0$ s (black lines, uniform array), $t_c=13.1$ s (green bars, vortex temporal location ${\overline{\xi }}_v=-10$), and $t_e=33.2$ s (purple bars, vortex temporal location ${\overline{\xi }}_v=-20$), fitting the dispersion presented in Fig. 5a, c, e, correspondingly. The vortex dispersion is illuminated by subplot (b), presenting the spatial density in a focused ordinate. The temporal location of the vortex is marked by dashed lines (color figure online)

Fig. 7

Downstream settling distances of $d_0=65$ $\mathrm{\mu }\text{m}$ saliva droplets dispersed by a vortex of $a=0.1$ m radius and ${\omega }_m=10{\text{s}}^{-1}$ initial maximal intensity, mapped as function of their initial location $(x_0,y_0)$ relative to the vortex location, denoted by a solid black line. The settling distance $\mathrm{\Delta }{x}_p$, and both axes, are normalized using the vortex radius a

Fig. 8

Downstream settling distances of saliva droplet (black line), water droplet (blue line), and solid particle (red line) with variable initial diameter, dispersed by a vortex of radius $a=0.1$ m and initial maximal intensity of ${\omega }_m=10{\text{s}}^{-1}$. The dashed line presents the dispersion generated by an ideal, inviscid vortex, whereas other solid lines mark the results of the viscid, decaying wake. All tracked particles were released from $(-3,3)$ relative to the vortex center. The double-critical behavior is illuminated by subplot (b), presenting the settling distances in a focused ordinate (color figure online)

Fig. 9

Downstream settling distances of $d_0=75$ $\mathrm{\mu }\text{m}$ saliva droplet (black line), water droplet (blue line), and solid particle (red line), dispersed by a vortex of $a=0.1$ m radius and variable initial maximal intensity. The dashed line presents the dispersion generated by an ideal, inviscid vortex, whereas other solid lines mark the results of the viscid, decaying wake. All tracked particles are released from $(-3,3)$ relative to the vortex center. The double-critical behavior is illuminated by subplot (b), presenting the settling distances in a focused ordinate

Fig. 10

Downstream settling distances of $d_0=75$ $\mathrm{\mu }\text{m}$ saliva droplet (black line), water droplet (blue line), and solid particle (red line), dispersed by a vortex of ${\omega }_m=10{\text{s}}^{-1}$ initial maximal intensity and variable radius. The dashed line presents the dispersion generated by an ideal, inviscid vortex, whereas other solid lines mark the results of the viscid, decaying wake. All tracked particles were released from $(-3,3)$ relative to the vortex center. The double-critical behavior is illuminated by subplot (b), presenting the settling distances in a focused ordinate (color figure online)

Fig. 11

Comparison of evaporating saliva droplets’ critical trajectories. Left-hand side subplots (a,c,e) present the trajectories of the droplets in the vortex frame of reference, while the right-hand side subplots (c,d,f) show the same trajectories relative to the ground. The conditions for which each trajectory is found are listed in Table 2