Statistical perspective on functional and causal neural connectomics: The Time-Aware PC algorithm

Abstract

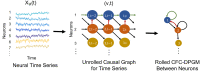
The representation of the flow of information between neurons in the brain based on their activity is termed the causal functional connectome. Such representation incorporates the dynamic nature of neuronal activity and causal interactions between them. In contrast to connectome, the causal functional connectome is not directly observed and needs to be inferred from neural time series. A popular statistical framework for inferring causal connectivity from observations is the directed probabilistic graphical modeling. Its common formulation is not suitable for neural time series since it was developed for variables with independent and identically distributed static samples. In this work, we propose to model and estimate the causal functional connectivity from neural time series using a novel approach that adapts directed probabilistic graphical modeling to the time series scenario. In particular, we develop the Time-Aware PC (TPC) algorithm for estimating the causal functional connectivity, which adapts the PC algorithm-a state-of-the-art method for statistical causal inference. We show that the model outcome of TPC has the properties of reflecting causality of neural interactions such as being non-parametric, exhibits the directed Markov property in a time-series setting, and is predictive of the consequence of counterfactual interventions on the time series. We demonstrate the utility of the methodology to obtain the causal functional connectome for several datasets including simulations, benchmark datasets, and recent multi-array electro-physiological recordings from the mouse visual cortex.

Fig 1. Causal modeling of neural time series.

Schematic depiction of causal modeling of the neural time series (left) by the Unrolled Causal Graph (middle), and then rolling back its edges (colored) to define the Rolled CFC-DPGM (right).

Fig 2. The TPC algorithm.

Illustration of Steps 1–7 in the TPC Algorithm: Time Advance, Bootstrap, PC, Orient, Rolled CFC-DPGM, Robust edges and Pruning.

Fig 3. Comparative study of CFC inference.

(a) CFC inference by GC, DPGM, and TPC, is compared on three examples of motifs and simulation paradigms; from left to right: Linear Gaussian, Non-linear Non-Gaussian, CTRNN. Table: 4-neurons motifs that define the Ground Truth CFC (row 1) are depicted along with inferred CFC over several simulation instances according to the three different methods (row 2–4). Each inferred CFC has an edge v → w that corresponds to an edge detected in any of the inference instances. The percentage (blue) next to each edge indicates the number of times the edge was detected out of all instances. (b) IFPR (green), TP rate (orange) and Combined Score (purple) of each method are shown for each motif.

Fig 4. Comparative study over levels of noise and thresholding parameter.

Combined Score of the three methods of CFC inference—TPC (red), DPGM (blue), GC (gray), over varying noise levels in simulation η = 0.1, 0.5, 1.0, …, 3.5, for simulated motifs from Linear Gaussian, Non-linear Non-Gaussian and CTRNN paradigms (left to right), with thresholding parameter α = 0.01, 0.05, 0.1 (top to bottom).

Fig 5. Interventional connectivity weights.

Inference of interventional connectivity weights by the TPC algorithm with max delay 1 msec for the example motifs from the three simulation paradigms: Linear Gaussian VAR, Non-linear Non-Gaussian VAR, CTRNN (left to right). Top row: Ground Truth CFC with excitatory (red) and inhibitory (green) connections; Bottom row: Estimated CFC labeled with edge weights (median [min,max] over all instances) and inferred nature whether excitatory (red) or inhibitory (green).

Fig 6. Application to Neuropixels dataset.

Comparison and demonstration of the FC inferred for a benchmark of mice brain data from the Allen Institute’s Neuropixels dataset, by three methods for FC inference: Associative FC using Sparse Partial Correlation, and Causal FC using GC and TPC. The estimated FC is represented by its adjacency matrix with edge weights, which is symmetric for Associative FC and asymmetric for Causal FC. The mice were subject to different stimuli, among which we selected four stimuli categories with distinct characteristics: Natural Scenes, Static Gratings, Gabor Patches and Full-Field Flashes [43]. The neurons are clustered by the region of brain: Visual Cortex, Hippo-Campal Formation, and Thalamus, which are further divided into sub-regions. In the adjacency matrices, a non-zero entry in (i, j) represents the connection of neuron i → j.

Fig 7. Graphical comparison of estimated CFC over stimuli.

This figure compares the distribution of graph measures of CFC obtained by TPC over different stimuli: natural scenes, static gratings, Gabor patches and flashes. The distribution for each graph measure and stimuli is shown by a boxplot.

Fig 8. Impact of intervention.

Rolled CFC-DPGM (left) for neurons 1–4 with dynamics as in Example 5.1, and consequence of intervention on neurons labelled A and B by (i) Ablation of A and (ii) External modulation of B.