A set-theoretic definition of cell types with an algebraic structure on gene regulatory networks and application in annotation of RNA-seq data

Abstract

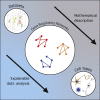
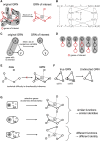
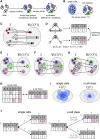
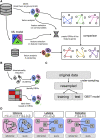
The emergence of single-cell RNA sequencing (RNA-seq) has radically changed the observation of cellular diversity. Although annotations of RNA-seq data require preserved properties among cells of an identity, annotations using conventional methods have not been able to capture universal characters of a cell type. Analysis of expression levels cannot be accurately annotated for cells because differences in transcription do not necessarily explain biological characteristics in terms of cellular functions and because the data themselves do not inform about the correct mapping between cell types and genes. Hence, in this study, we developed a new representation of cellular identities that can be compared over different datasets while preserving nontrivial biological semantics. To generalize the notion of cell types, we developed a new framework to manage cellular identities in terms of set theory. We provided further insights into cells by installing mathematical descriptions of cell biology. We also performed experiments that could correspond to practical applications in annotations of RNA-seq data.

Keywords: annotation; cell type; cellular state; mathematical model; scRNA-seq; set theory; transcriptome.

Graphical abstract

Figure 1

The GEN as a universal model of causality for gene expression and the possessed cascades as observed relationships of the genes (A) Schematic of the GEN. The vertexes denote genes, and the edges denote causality. A latent variable $\text{ε}$ for extrinsic factors is present in the center of the illustration. (B) $\text{ε}$ as the Cartesian product of the exogenous variables for the corresponding vertex in the causal graphical model. (C) Causality blockade altering the relationship between two variables. When the variable y is unobserved, the path between x and z remains (i.e., x and z are mutually dependent on each other). In contrast, when the observation fixes the y value, the path between x and z is blocked (i.e., the two variables are mutually independent). (D) Graphical explanation of the GEN and a GRN.

Figure 2

Mathematical operations required to simplify the GRN (A) A conceptual illustration of excluding genes from the GRN. (B) Graphs of the genes of interest are induced subgraphs of the graph featuring all genes. (C) An operation to remove genes from GRNs, which is equivalent to treating the genes as exogenous variables. (D) Cascades and vertexes treated as exogenous variables. Shaded areas are neglected in the simplified GRN. (E) Technical difficulties of data-driven causal exploration. (F) Effect of conversion from directed to undirected edges. (G) Comparison of cellular identities using undirected GRNs.

Figure 3

Topological spaces of cellular similarity (A) Standard workflow of scRNA-seq analysis. (B) Using the same metric to compare single cells and cell classes, which is nontrivial. (C) Morphism that maps single cells to the corresponding GRNs. (D) Structural similarity of single cells’ GRNs, which is equivalent to the Hamming distance for strings of 0 and 1. (E–G) Quotient spaces of cell classes. The shaded areas in $S$ are cell classes, and those in $\mathfrak{P}\left(C\left(F\right)\right)$ are images of $\phi$ pertaining to the cell classes. (H) Graphical explanation of the statement regarding the choice of representative GRNs from a cell class. (I) The GRN of a cell class, approximately regarded as the intersection GRN for all single cells in the cell class. (J) The inclusion relations of eigen-cascades, indicating the structural similarity of GRNs in the case of cell classes.

Figure 4

Overview of analyses used in this research (A) Workflow of GRN-based cell-class annotation, using FA and an ML model. (B) Standard workflow of the conventional annotation using DEGs. (C) Overview of data splitting. (D) Schematics of the three GRN-based annotation methods: inference, labeling, and estimation.

Figure 5

A GBDT model to identify features with which to classify cell types in m1_10x (A) A scatterplot of the uniform manifold approximation and projection (UMAP) manifold on expression patterns of the 90 marker genes in m1_10x. The marker colors denote cell types given in the metadata. (B) Sample ratio transition during resampling and data splitting. (C and D) SD among the group-wise mean values of gene expression. (E) Subclass information given in the metadata of m1_10x. (F) Top 10 genes (in terms of the median of FI) during 5-fold hyperparameter tuning. (G and H) ROC curve and PR curve of the GBDT model with the top 1,000 genes (in terms of SD among the group-wise means). AUC, AP, and the macro or micro averages thereof were also calculated. (I and J) The evaluation metrics for the GBDT model with GAD1 and GRIP1.

Figure 6

and k-means in GSE165388 (A–D) The parallel analyses used to determine the number of factors in gw9–gw12. (E–H) Heatmaps of factor loadings after elimination of factors with maximum loadings smaller than 0.5. Quartimin rotation was performed for all models. (I–L) Silhouette plots for optimal k values. (M−P) Results of k-means clustering in UMAP.

Figure 7

GRN-based annotation in GSE165388 (A) GRNs of cell types in m1_10x to be used in labeling (as the referential data). (B–E) GRNs of all clusters in gw9–gw12. All vertexes and edges used in labeling or estimation are indicated. (F–H) “Planet plots” showing the labeling results. The referential cell classes are shown in the center, and the circles’ radii denote values of $d^{\ast }$. The cell classes on the innermost circles are considered to be most similar to those in the center. (I) Comparison of DEG- and GRN-based annotation methods.