Deep learning to decompose macromolecules into independent Markovian domains
- PMID: 36402768
- PMCID: PMC9675806
- DOI: 10.1038/s41467-022-34603-z
Deep learning to decompose macromolecules into independent Markovian domains
Abstract
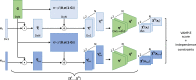
The increasing interest in modeling the dynamics of ever larger proteins has revealed a fundamental problem with models that describe the molecular system as being in a global configuration state. This notion limits our ability to gather sufficient statistics of state probabilities or state-to-state transitions because for large molecular systems the number of metastable states grows exponentially with size. In this manuscript, we approach this challenge by introducing a method that combines our recent progress on independent Markov decomposition (IMD) with VAMPnets, a deep learning approach to Markov modeling. We establish a training objective that quantifies how well a given decomposition of the molecular system into independent subdomains with Markovian dynamics approximates the overall dynamics. By constructing an end-to-end learning framework, the decomposition into such subdomains and their individual Markov state models are simultaneously learned, providing a data-efficient and easily interpretable summary of the complex system dynamics. While learning the dynamical coupling between Markovian subdomains is still an open issue, the present results are a significant step towards learning Ising models of large molecular complexes from simulation data.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures




Similar articles
-
VAMPnets for deep learning of molecular kinetics.Nat Commun. 2018 Jan 2;9(1):5. doi: 10.1038/s41467-017-02388-1. Nat Commun. 2018. PMID: 29295994 Free PMC article.
-
Independent Markov decomposition: Toward modeling kinetics of biomolecular complexes.Proc Natl Acad Sci U S A. 2021 Aug 3;118(31):e2105230118. doi: 10.1073/pnas.2105230118. Proc Natl Acad Sci U S A. 2021. PMID: 34321356 Free PMC article.
-
Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics.J Chem Phys. 2007 Apr 21;126(15):155101. doi: 10.1063/1.2714538. J Chem Phys. 2007. PMID: 17461665
-
Markov field models: Scaling molecular kinetics approaches to large molecular machines.Curr Opin Struct Biol. 2022 Dec;77:102458. doi: 10.1016/j.sbi.2022.102458. Epub 2022 Sep 23. Curr Opin Struct Biol. 2022. PMID: 36162297 Review.
-
Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine Learning.JACS Au. 2021 Aug 4;1(9):1330-1341. doi: 10.1021/jacsau.1c00254. eCollection 2021 Sep 27. JACS Au. 2021. PMID: 34604842 Free PMC article. Review.
Cited by
-
AMUSET-TICA: A Tensor-Based Approach for Identifying Slow Collective Variables in Biomolecular Dynamics.J Chem Theory Comput. 2025 May 13;21(9):4855-4866. doi: 10.1021/acs.jctc.5c00076. Epub 2025 Apr 20. J Chem Theory Comput. 2025. PMID: 40254940
-
Memory kernel minimization-based neural networks for discovering slow collective variables of biomolecular dynamics.Nat Comput Sci. 2025 Jul;5(7):562-571. doi: 10.1038/s43588-025-00815-8. Epub 2025 Jun 10. Nat Comput Sci. 2025. PMID: 40495006
-
Thermodynamic Interpolation: A Generative Approach to Molecular Thermodynamics and Kinetics.J Chem Theory Comput. 2025 Mar 11;21(5):2535-2545. doi: 10.1021/acs.jctc.4c01557. Epub 2025 Feb 23. J Chem Theory Comput. 2025. PMID: 39988824 Free PMC article.
-
Exploring and Learning the Universe of Protein Allostery Using Artificial Intelligence Augmented Biophysical and Computational Approaches.J Chem Inf Model. 2023 Mar 13;63(5):1413-1428. doi: 10.1021/acs.jcim.2c01634. Epub 2023 Feb 24. J Chem Inf Model. 2023. PMID: 36827465 Free PMC article. Review.
-
Special Issue: "Advanced Research on Molecular Modeling of Protein Structure and Functions".Int J Mol Sci. 2025 Aug 16;26(16):7916. doi: 10.3390/ijms26167916. Int J Mol Sci. 2025. PMID: 40869235 Free PMC article.
References
-
- Vant, J. W. et al. Protein Structure Prediction 301–315 (Springer, 2020).
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

