Moving the needle: Employing deep reinforcement learning to push the boundaries of coarse-grained vaccine models

Abstract

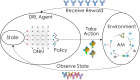
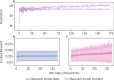
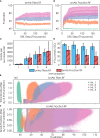
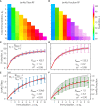
Highly mutable infectious disease pathogens (hm-IDPs) such as HIV and influenza evolve faster than the human immune system can contain them, allowing them to circumvent traditional vaccination approaches and causing over one million deaths annually. Agent-based models can be used to simulate the complex interactions that occur between immune cells and hm-IDP-like proteins (antigens) during affinity maturation-the process by which antibodies evolve. Compared to existing experimental approaches, agent-based models offer a safe, low-cost, and rapid route to study the immune response to vaccines spanning a wide range of design variables. However, the highly stochastic nature of affinity maturation and vast sequence space of hm-IDPs render brute force searches intractable for exploring all pertinent vaccine design variables and the subset of immunization protocols encompassed therein. To address this challenge, we employed deep reinforcement learning to drive a recently developed agent-based model of affinity maturation to focus sampling on immunization protocols with greater potential to improve the chosen metrics of protection, namely the broadly neutralizing antibody (bnAb) titers or fraction of bnAbs produced. Using this approach, we were able to coarse-grain a wide range of vaccine design variables and explore the relevant design space. Our work offers new testable insights into how vaccines should be formulated to maximize protective immune responses to hm-IDPs and how they can be minimally tailored to account for major sources of heterogeneity in human immune responses and various socioeconomic factors. Our results indicate that the first 3 to 5 immunizations, depending on the metric of protection, should be specially tailored to achieve a robust protective immune response, but that beyond this point further immunizations require only subtle changes in formulation to sustain a durable bnAb response.

Keywords: HIV - human immunodeficiency virus; affinity maturation; agent-based modelling; deep reinforcement learning (Deep RL); immunovirology; multiscale (MS) modelling; vaccine design protocol.

Figure 1

Overview of how deep reinforcement learning (DRL) is coupled to the agent-based model of affinity maturation (AM) in the current work. The DRL agent chooses an action (here, the level of vaccine-imposed frustration, modulated by changing antigen sequence and/or concentration) that is fed into the environment (here, the AM process), after which the agent observes the state of the system (here, properties of the vaccine-induced memory B cell receptor/antibody population). The agent then receives a reward based on how well the observed state meets a user-defined reward metric (here, the quality and quantity of the resulting plasma B cell receptor/antibody population). Over time, the agent learns a robust mapping between the states and actions, leading to an optimal policy (here, a vaccination/temporal frustration protocol) for maximizing the chosen reward.

Figure 2

Broad overview of the affinity maturation (AM) process by which antibodies (Abs) evolve against vaccine-candidate antigens (Ags) in a germinal center (GC) reaction (see text for details). Here, we administered between one and ten total immunizations, N _T , of a single Ag, varying only the Ag concentration, c _Ag , in each immunization (indicated by the different shades of the Ags).

Figure 3

Convergence profiles of (A) the level of frustration imposed on GC reactions in the first vaccine immunization, as chosen by the DRL agent, and (B, C) the corresponding scaled reward values obtained by the DRL agent. Results are shown in blue for the bnAb titers reward function, and in pink for the bnAb fraction reward function. The data shown represents a rolling average with 500 DRL steps for both the mean and standard deviation (shown in lighter colors).

Figure 4

Convergence of frustration values F ₁ (green), F ₂ (orange), F ₃ (purple), and F ₄ (pink) for (A) the bnAb titers reward function (RF) and (B) the bnAb fraction RF, across four total immunizations; (C) bnAb titers produced per successful GC (out of n=100 GCs) for both RFs after each of the four immunizations; (D) number of successfully terminating GCs after each immunization for both RFs; (E) distribution of bnAb titer response for a given F _i after the four immunizations; and (F) fractional bnAb response for a given F _i after the four immunizations. In (A, B), the rolling average +/- the rolling standard deviation is plotted using 500 DRL steps. In (C, D), error bars are +/- the standard deviation of the respective metric (bnAb titers/successful GC and total successful GCs, respectively). In (E, F), the y-values shown are the responses after administering all four immunizations; that is, the y-values are plotted as (F _i∈4, ℛ ₄) for ℛ ₄≡ total bnAb titers and bnAb fraction, respectively.

Figure 5

Frustration values of a given immunization, i , out of a total number of immunizations, N _T , where the column corresponds to the i ^th immunization, and the row corresponds to the total immunizations for both the (A) bnAb titers reward function and (B) bnAb fraction reward function; the average frustration for a given immunization, F _i , averaged across all N _T for (C) the bnAb titers reward function (purple) and (D) the bnAb fraction reward function (pink), with their respective Michaelis-Menten saturation fits (red) +/- the standard deviation (gray); the average reward for a given immunization, ℛ _i , for the bnAb titers reward function (E, blue) and bnAb fraction reward function (F, green), with their respective fits (red) and standard deviation of the fit (gray). In (C–F), the error bars represent the standard deviation. Fitted parameters for the Michaelis-Menten model are shown in (C–F).