Time-delayed modelling of the COVID-19 dynamics with a convex incidence rate

Abstract

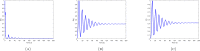
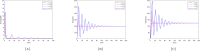
COVID-19 pandemic represents an unprecedented global health crisis which has an enormous impact on the world population and economy. Many scientists and researchers have combined efforts to develop an approach to tackle this crisis and as a result, researchers have developed several approaches for understanding the COVID-19 transmission dynamics and the way of mitigating its effect. The implementation of a mathematical model has proven helpful in further understanding the behaviour which has helped the policymaker in adopting the best policy necessary for reducing the spread. Most models are based on a system of equations which assume an instantaneous change in the transmission dynamics. However, it is believed that SARS-COV-2 have an incubation period before the tendency of transmission. Therefore, to capture the dynamics adequately, there would be a need for the inclusion of delay parameters which will account for the delay before an exposed individual could become infected. Hence, in this paper, we investigate the SEIR epidemic model with a convex incidence rate incorporated with a time delay. We first discussed the epidemic model as a form of a classical ordinary differential equation and then the inclusion of a delay to represent the period in which the susceptible and exposed individuals became infectious. Secondly, we identify the disease-free together with the endemic equilibrium state and examine their stability by adopting the delay differential equation stability theory. Thereafter, we carried out numerical simulations with suitable parameters choice to illustrate the theoretical result of the system and for a better understanding of the model dynamics. We also vary the length of the delay to illustrate the changes in the model as the delay parameters change which enables us to further gain an insight into the effect of the included delay in a dynamical system. The result confirms that the inclusion of delay destabilises the system and it forces the system to exhibit an oscillatory behaviour which leads to a periodic solution and it further helps us to gain more insight into the transmission dynamics of the disease and strategy to reduce the risk of infection.

Keywords: 34D20; 37N25; 39A60; 92B05; COVID-19; Convex incidence rate; Delay differential equation; SEIR epidemic model; Stability.

Fig. 1

Flowchart of an SEIR epidemic model with convex incidence rate without delay.

Fig. 2

Delayed SEIR epidemic model with convex incidence rate flow chart.

Fig. 3

Time series plot for $\tau =1.70$.

Fig. 4

Effect of time delay $\tau$ on the model dynamics.

Fig. 5

Model phase plane.