Social dilemmas of sociality due to beneficial and costly contagion
- PMID: 36409767
- PMCID: PMC9721494
- DOI: 10.1371/journal.pcbi.1010670
Social dilemmas of sociality due to beneficial and costly contagion
Abstract
Levels of sociality in nature vary widely. Some species are solitary; others live in family groups; some form complex multi-family societies. Increased levels of social interaction can allow for the spread of useful innovations and beneficial information, but can also facilitate the spread of harmful contagions, such as infectious diseases. It is natural to assume that these contagion processes shape the evolution of complex social systems, but an explicit account of the dynamics of sociality under selection pressure imposed by contagion remains elusive. We consider a model for the evolution of sociality strategies in the presence of both a beneficial and costly contagion. We study the dynamics of this model at three timescales: using a susceptible-infectious-susceptible (SIS) model to describe contagion spread for given sociality strategies, a replicator equation to study the changing fractions of two different levels of sociality, and an adaptive dynamics approach to study the long-time evolution of the population level of sociality. For a wide range of assumptions about the benefits and costs of infection, we identify a social dilemma: the evolutionarily-stable sociality strategy (ESS) is distinct from the collective optimum-the level of sociality that would be best for all individuals. In particular, the ESS level of social interaction is greater (respectively less) than the social optimum when the good contagion spreads more (respectively less) readily than the bad contagion. Our results shed light on how contagion shapes the evolution of social interaction, but reveals that evolution may not necessarily lead populations to social structures that are good for any or all.
Copyright: © 2022 Cooney et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
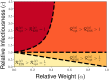
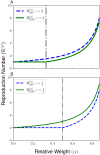
Similar articles
-
Social information use shapes the coevolution of sociality and virulence.Evolution. 2022 Jun;76(6):1153-1169. doi: 10.1111/evo.14491. Epub 2022 Apr 23. Evolution. 2022. PMID: 35420704 Free PMC article.
-
Co-evolution between sociality and dispersal: the role of synergistic cooperative benefits.J Theor Biol. 2012 Nov 7;312:44-54. doi: 10.1016/j.jtbi.2012.07.016. Epub 2012 Jul 25. J Theor Biol. 2012. PMID: 22841740
-
Social contagion in primates: Moderating factors and significance for individuals and the group.Neurosci Biobehav Rev. 2025 Jun;173:106156. doi: 10.1016/j.neubiorev.2025.106156. Epub 2025 Apr 16. Neurosci Biobehav Rev. 2025. PMID: 40250542 Review.
-
"Emotional Proximity" and "Spatial Proximity": Higher Relationship Quality and Nearer Distance Both Strengthen Scratch Contagion in Tibetan Macaques.Animals (Basel). 2022 Aug 22;12(16):2151. doi: 10.3390/ani12162151. Animals (Basel). 2022. PMID: 36009741 Free PMC article.
-
Stay social, stay young: a bioanthropological outlook on the processes linking sociality and ageing.Geroscience. 2025 Feb;47(1):721-744. doi: 10.1007/s11357-024-01416-5. Epub 2024 Nov 11. Geroscience. 2025. PMID: 39527178 Free PMC article. Review.
Cited by
-
Beyond collective intelligence: Collective adaptation.J R Soc Interface. 2023 Mar;20(200):20220736. doi: 10.1098/rsif.2022.0736. Epub 2023 Mar 22. J R Soc Interface. 2023. PMID: 36946092 Free PMC article. Review.
-
The Impact of Social Participation on Frailty among Older Adults: The Mediating Role of Loneliness and Sleep Quality.Healthcare (Basel). 2024 Oct 18;12(20):2085. doi: 10.3390/healthcare12202085. Healthcare (Basel). 2024. PMID: 39451499 Free PMC article.
-
The role of social attraction and social avoidance in shaping modular networks.R Soc Open Sci. 2024 Feb 28;11(2):231619. doi: 10.1098/rsos.231619. eCollection 2024 Feb. R Soc Open Sci. 2024. PMID: 38420628 Free PMC article.
-
Dynamics in a behavioral-epidemiological model for individual adherence to a nonpharmaceutical intervention.Proc Natl Acad Sci U S A. 2023 Oct 31;120(44):e2311584120. doi: 10.1073/pnas.2311584120. Epub 2023 Oct 27. Proc Natl Acad Sci U S A. 2023. PMID: 37889930 Free PMC article.
-
The contribution of movement to social network structure and spreading dynamics under simple and complex transmission.Philos Trans R Soc Lond B Biol Sci. 2024 Oct 21;379(1912):20220524. doi: 10.1098/rstb.2022.0524. Epub 2024 Sep 4. Philos Trans R Soc Lond B Biol Sci. 2024. PMID: 39230450 Free PMC article.
References
-
- Rubenstein DR, Abbot P. The evolution of social evolution. In: Rubenstein DR, Abbot P, editors. Comparative social evolution. Cambridge: Cambridge University Press; 2017. p. 1–18.
-
- Alexander RD. The evolution of social behavior. Annual Review of Ecology and Systematics. 1974; 5(1):325–83. doi: 10.1146/annurev.es.05.110174.001545 - DOI
-
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character. 1927 Aug 1;115(772):700–21.
-
- Bass FM. A new product growth for model consumer durables. Management Science. 1969. Jan;15(5):215–27. doi: 10.1287/mnsc.15.5.215 - DOI
-
- Rogers EM. Diffusion of Innovations. 4th ed. New York: Simon and Schuster; 2010. Jul 6.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

