Modeling Rapid Guessing Behaviors in Computer-Based Testlet Items

Abstract

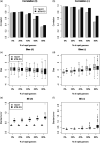
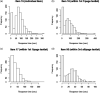
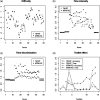
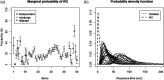
In traditional test models, test items are independent, and test-takers slowly and thoughtfully respond to each test item. However, some test items have a common stimulus (dependent test items in a testlet), and sometimes test-takers lack motivation, knowledge, or time (speededness), so they perform rapid guessing (RG). Ignoring the dependence in responses to testlet items can negatively bias standard errors of measurement, and ignoring RG by fitting a simpler item response theory (IRT) model can bias the results. Because computer-based testing captures response times on testlet responses, we propose a mixture testlet IRT model with item responses and response time to model RG behaviors in computer-based testlet items. Two simulation studies with Markov chain Monte Carlo estimation using the JAGS program showed (a) good recovery of the item and person parameters in this new model and (b) the harmful consequences of ignoring RG (biased parameter estimates: overestimated item difficulties, underestimated time intensities, underestimated respondent latent speed parameters, and overestimated precision of respondent latent estimates). The application of IRT models with and without RG to data from a computer-based language test showed parameter differences resembling those in the simulations.

Keywords: mixture model; multidimensional item response theory; rapid guessing, testlet; response time.

Figure 1.

Correlation, bias, and standard error of person estimates for the TM-RT and MTM-RG in Simulation 2.

Figure 2.

Histogram of RTs in the reading test. Note. The mean RT on the 3^rd all/page testlet was used to draw Figure 2d.

Figure 3.

Item parameter estimates for the TM-RT and MTM-RG in the reading test. Note. The 1^st, 2^nd, and 14^th testlets are presented in the one/page design. They are items 1–6, 7–12, and 45–50, respectively.

Figure 4.

Marginal probability of RG and the probability density functions of RT under the MTM-RG in the reading test. Note. The three all/page testlets are items 1–6, 7–12, and 45–50. The upper and lower bounds define the 95% probability interval. The all/page testlets are excluded in Figure 4b.