Self-Diffusion in Confined Water: A Comparison between the Dynamics of Supercooled Water in Hydrophobic Carbon Nanotubes and Hydrophilic Porous Silica
- PMID: 36430907
- PMCID: PMC9697084
- DOI: 10.3390/ijms232214432
Self-Diffusion in Confined Water: A Comparison between the Dynamics of Supercooled Water in Hydrophobic Carbon Nanotubes and Hydrophilic Porous Silica
Abstract
Confined liquids are model systems for the study of the metastable supercooled state, especially for bulk water, in which the onset of crystallization below 230 K hinders the application of experimental techniques. Nevertheless, in addition to suppressing crystallization, confinement at the nanoscale drastically alters the properties of water. Evidently, the behavior of confined water depends critically on the nature of the confining environment and the interactions of confined water molecules with the confining matrix. A comparative study of the dynamics of water under hydrophobic and hydrophilic confinement could therefore help to clarify the underlying interactions. As we demonstrate in this work using a few representative results from the relevant literature, the accurate assessment of the translational mobility of water molecules, especially in the supercooled state, can unmistakably distinguish between the hydrophilic and hydrophobic nature of the confining environments. Among the numerous experimental methods currently available, we selected nuclear magnetic resonance (NMR) in a field gradient, which directly measures the macroscopic translational self-diffusion coefficient, and quasi-elastic neutron scattering (QENS), which can determine the microscopic translational dynamics of the water molecules. Dielectric relaxation, which probes the re-orientational degrees of freedom, are also discussed.
Keywords: MCM-41; NMR; QENS; carbon nanotubes; molecule dynamics; supercooled water.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
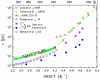
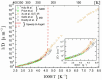
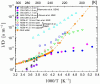
 ), dark grey triangles (
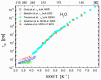
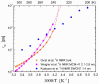
), dark grey triangles ( ), and stars (★) are the D values of H2O confined in SW 1.1 nm, MW 3.0 nm, and DW 3.5 nm, respectively, acquired via 2D D-T2 static field gradient NMR experiments (Gkoura et al. [74]). Inverted open triangles (▽) are the self-diffusion coefficients obtained from the pulsed field gradient NMR experiments of water confined in MCM-41 (Chen et al. [75]). Open circles (◯), open squares (□), and open upright triangles (△) are the self-diffusion coefficients obtained from static field gradient NMR experiments on water in open 2.8 nm, capped 2.8 nm, and capped 2.1 nm MCM-41 samples, respectively (Weigler et al. [76]).
), and stars (★) are the D values of H2O confined in SW 1.1 nm, MW 3.0 nm, and DW 3.5 nm, respectively, acquired via 2D D-T2 static field gradient NMR experiments (Gkoura et al. [74]). Inverted open triangles (▽) are the self-diffusion coefficients obtained from the pulsed field gradient NMR experiments of water confined in MCM-41 (Chen et al. [75]). Open circles (◯), open squares (□), and open upright triangles (△) are the self-diffusion coefficients obtained from static field gradient NMR experiments on water in open 2.8 nm, capped 2.8 nm, and capped 2.1 nm MCM-41 samples, respectively (Weigler et al. [76]).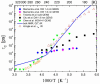
Similar articles
-
Neutron scattering study on dynamics of water molecules in MCM-41. 2. Determination of translational diffusion coefficient.J Phys Chem B. 2005 Jun 9;109(22):11231-9. doi: 10.1021/jp046036l. J Phys Chem B. 2005. PMID: 16852371
-
Structural studies of water in hydrophilic and hydrophobic mesoporous silicas: an x-ray and neutron diffraction study at 297 K.J Chem Phys. 2011 Feb 14;134(6):064509. doi: 10.1063/1.3530584. J Chem Phys. 2011. PMID: 21322707
-
Nanoscale dynamics of water confined in ordered mesoporous carbon.Phys Chem Chem Phys. 2019 Apr 17;21(16):8517-8528. doi: 10.1039/c8cp07704e. Phys Chem Chem Phys. 2019. PMID: 30957810 Free PMC article.
-
Self-diffusion studies by intra- and inter-molecular spin-lattice relaxometry using field-cycling: Liquids, plastic crystals, porous media, and polymer segments.Prog Nucl Magn Reson Spectrosc. 2017 Aug;101:18-50. doi: 10.1016/j.pnmrs.2017.04.001. Epub 2017 Apr 9. Prog Nucl Magn Reson Spectrosc. 2017. PMID: 28844220 Review.
-
A Multi-Scale Study of Water Dynamics under Confinement, Exploiting Numerical Simulations in Relation to NMR Relaxometry, PGSE and NMR Micro-Imaging Experiments: An Application to the Clay/Water Interface.Int J Mol Sci. 2020 Jun 30;21(13):4697. doi: 10.3390/ijms21134697. Int J Mol Sci. 2020. PMID: 32630160 Free PMC article. Review.
Cited by
-
Investigation of Dynamic Behavior of Confined Ionic Liquid [BMIM]+[TCM]- in Silica Material SBA-15 Using NMR.Int J Mol Sci. 2023 Apr 4;24(7):6739. doi: 10.3390/ijms24076739. Int J Mol Sci. 2023. PMID: 37047711 Free PMC article.
References
-
- Speedy R.J., Angell C.A. Isothermal compressibility of supercooled water and evidence for a thermodynamic singularity at −45 °C. J. Chem. Phys. 1976;65:851–858. doi: 10.1063/1.433153. - DOI
-
- Lang E.W., Lüdemann H.-D. Anomalies of Liquid Water. Angew. Chem. Int. Ed. 1982;21:315–329. doi: 10.1002/anie.198203153. - DOI
-
- Debenedetti P.G. Supercooled and glassy water. J. Phys. Condens. Matter. 2003;15:R1669–R1726. doi: 10.1088/0953-8984/15/45/R01. - DOI
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

