Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Nov 17;14(22):4985.
doi: 10.3390/polym14224985.

A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates

Aleksandr Elkin  1 , Viktor Gaibel  1 , Dmitry Dzhurinskiy  1 , Ivan Sergeichev  1
Affiliations

A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates

Aleksandr Elkin et al. Polymers (Basel). .

Abstract

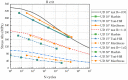
In the last decade, fatigue damage models for fiber-reinforced polymer composites have been developed assuming the fracture energy equivalence hypothesis. These models are able to predict a fatigue life of composite laminates, but their identification requires a significant number of off-axial tests for various stress ratios. The present study proposes the stress ratio dependent model, which phenomenologically adopts a decrease in stiffness and residual strength of a unique ply according to experimental constant life diagrams. Hashin, Tsai-Hill, and the maximum stress failure criteria are utilized for damage initiation considering the residual strength of the ply. The obtained results indicate a sufficiency of using S-N curves for UD 0°, UD 45°, and UD 90° for identification of the model. The model was verified by S-N curves for UD 10°, UD 15°, and UD 30° and its applicability was demonstrated for prediction of a fatigue life of composite laminates with an arbitrary lay-up. The model is implemented into ABAQUS finite element software as a user subroutine.

Keywords: damage initiation; fatigue; fiber-reinforced polymer composites; finite element analysis; residual strength.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Fatigue failure in multilayered FRPs: (a) Formation of cracks, i.e., damage accumulation; (b) Stiffness reduction for the described failure stages [14,15].
Figure 2
Figure 2
The CLD diagram illustration: A vertical axis—the alternate stress; A horizontal axis—the mean stress [21].
Figure 3
Figure 3
The FDM workflow.
Figure 4
Figure 4
Assumptions accepted: (a) Linear interpolation between S-N curves for a predefined R-ratios; (b) Proportional to stress stiffness reduction.
Figure 5
Figure 5
The samples geometry.
Figure 6
Figure 6
Approximated CLDs and S-N curves based on data [34] used in the FDM as lamina fatigue properties. S-N curves: (a) UD 0°, (c) UD 45°, (e) UD 90°. The CLDs: (b) UD 0°, (d) UD 45°, (f) UD 90°.
Figure 7
Figure 7
S-N curves used for verification of the FDM [29]: (a) UD 10°, (b) UD 15°, (c) UD 30°.
Figure 8
Figure 8
The finite element model for the FDM verification.
Figure 9
Figure 9
Comparison between experimental and predicted S-N curves of UD 10, 15, 30° for R = 0.1.
Figure 10
Figure 10
Comparison between experimental and predicted S-N curves of UD 10, 15, 30° for R = 10.
Figure 11
Figure 11
Comparison between experimental and predicted S-N curves of UD 10, 15, 30° for Rcrit (combined tension-compression mode).
See this image and copyright information in PMC

References

    1. Maskepatil L.P., Gandigude A.U., Kale S.A. Selection of Material for Wind Turbine Blade by Analytic Hierarchy Process (AHP) Method. Appl. Mech. Mater. 2014;612:145–150. doi: 10.4028/www.scientific.net/AMM.612.145. - DOI
    1. Sergeichev I., Fedulov B., Fedorenko A., Zershchikov K., Lomakin E., Akhatov I. Constitutive material model for the design and virtual testing of pressure vessel service equipment manufactured from thermoplastic fiber-reinforced polymer composites. Int. J. Press. Vessel. Pip. 2021;193:104475. doi: 10.1016/j.ijpvp.2021.104475. - DOI
    1. Vassilopoulos A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue. 2020;134:105512. doi: 10.1016/j.ijfatigue.2020.105512. - DOI
    1. Deng Q.-Y., Zhu S.-P., He J.-C., Li X.-K., Carpinteri A. Multiaxial fatigue under variable amplitude loadings: Review and solutions. Int. J. Struct. Integr. 2022;13:349–393. doi: 10.1108/IJSI-03-2022-0025. - DOI
    1. Liao D., Zhu S.-P., Qian G. Multiaxial fatigue analysis of notched components using combined critical plane and critical distance approach. Int. J. Mech. Sci. 2019;160:38–50. doi: 10.1016/j.ijmecsci.2019.06.027. - DOI

LinkOut - more resources