Dynamical modelling of street protests using the Yellow Vest Movement and Khabarovsk as case studies
- PMID: 36443352
- PMCID: PMC9705368
- DOI: 10.1038/s41598-022-23917-z
Dynamical modelling of street protests using the Yellow Vest Movement and Khabarovsk as case studies
Abstract
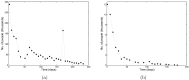
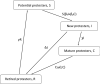
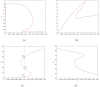
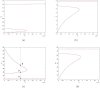
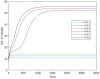
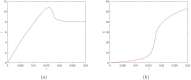
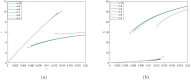
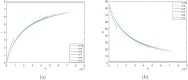
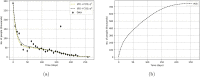
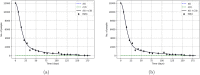
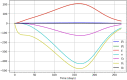
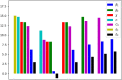
Social protests, in particular in the form of street protests, are a frequent phenomenon of modern world often making a significant disruptive effect on the society. Understanding the factors that can affect their duration and intensity is therefore an important problem. In this paper, we consider a mathematical model of protests dynamics describing how the number of protesters change with time. We apply the model to two events such as the Yellow Vest Movement 2018-2019 in France and Khabarovsk protests 2019-2020 in Russia. We show that in both cases our model provides a good description of the protests dynamics. We consider how the model parameters can be estimated by solving the inverse problem based on the available data on protesters number at different time. The analysis of parameter sensitivity then allows for determining which factor(s) may have the strongest effect on the protests dynamics.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures



Similar articles
-
The statistical and dynamic modeling of the first part of the 2013-2014 Euromaidan protests in Ukraine: The Revolution of Dignity and preceding times.PLoS One. 2024 May 28;19(5):e0301639. doi: 10.1371/journal.pone.0301639. eCollection 2024. PLoS One. 2024. PMID: 38805495 Free PMC article.
-
Understanding street protests: from a mathematical model to protest management.PLoS One. 2025 Apr 10;20(4):e0319837. doi: 10.1371/journal.pone.0319837. eCollection 2025. PLoS One. 2025. PMID: 40209167 Free PMC article.
-
A comparative analysis of the causes of the protests in Southern Africa.SN Soc Sci. 2023;3(2):28. doi: 10.1007/s43545-023-00613-x. Epub 2023 Jan 18. SN Soc Sci. 2023. PMID: 36691644 Free PMC article.
-
When Are Social Protests Effective?Trends Cogn Sci. 2024 Mar;28(3):252-263. doi: 10.1016/j.tics.2023.10.003. Epub 2023 Oct 31. Trends Cogn Sci. 2024. PMID: 37914605 Review.
-
The pros and cons of researching events ethnographically.Ethnography. 2017 Sep;18(3):415-424. doi: 10.1177/1466138117709293. Epub 2017 May 16. Ethnography. 2017. PMID: 29081715 Free PMC article. Review.
Cited by
-
The statistical and dynamic modeling of the first part of the 2013-2014 Euromaidan protests in Ukraine: The Revolution of Dignity and preceding times.PLoS One. 2024 May 28;19(5):e0301639. doi: 10.1371/journal.pone.0301639. eCollection 2024. PLoS One. 2024. PMID: 38805495 Free PMC article.
-
Understanding street protests: from a mathematical model to protest management.PLoS One. 2025 Apr 10;20(4):e0319837. doi: 10.1371/journal.pone.0319837. eCollection 2025. PLoS One. 2025. PMID: 40209167 Free PMC article.
References
-
- Handler JF. Postmodernism, protest, and the new social movements. Law Soc. Rev. 1992;26(4):697–731. doi: 10.2307/3053811. - DOI
-
- Haynes MJ. Patterns of conflict in the 1905 revolution. In: Glatter P, editor. The Russian Revolution of 1905: Change Through Struggle. Porcupine Press; 2005. pp. 215–233.
-
- Roberts A, Garton Ash T, editors. Civil Resistance and Power Politics: The Experience of Non-violent Action from Gandhi to the Present. Oxford University Press; 2009.
-
- Dalton R, Van Sickle A, Weldon S. The individual-institutional nexus of protest behaviour. Br. J. Polit. Sci. 2010;40(1):51–73. doi: 10.1017/S000712340999038X. - DOI
-
- Seferiades S, Johnston H, editors. Violent Protest, Contentious Politics, and the Neoliberal State. Ashgate Publishing; 2012.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

