Sampling effects and measurement overlap can bias the inference of neuronal avalanches
- PMID: 36445932
- PMCID: PMC9733887
- DOI: 10.1371/journal.pcbi.1010678
Sampling effects and measurement overlap can bias the inference of neuronal avalanches
Abstract
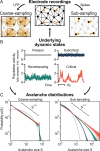
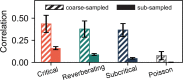
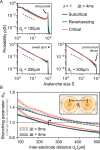
To date, it is still impossible to sample the entire mammalian brain with single-neuron precision. This forces one to either use spikes (focusing on few neurons) or to use coarse-sampled activity (averaging over many neurons, e.g. LFP). Naturally, the sampling technique impacts inference about collective properties. Here, we emulate both sampling techniques on a simple spiking model to quantify how they alter observed correlations and signatures of criticality. We describe a general effect: when the inter-electrode distance is small, electrodes sample overlapping regions in space, which increases the correlation between the signals. For coarse-sampled activity, this can produce power-law distributions even for non-critical systems. In contrast, spike recordings do not suffer this particular bias and underlying dynamics can be identified. This may resolve why coarse measures and spikes have produced contradicting results in the past.
Copyright: © 2022 Pinheiro Neto et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures




Similar articles
-
The recovery of parabolic avalanches in spatially subsampled neuronal networks at criticality.Sci Rep. 2024 Aug 20;14(1):19329. doi: 10.1038/s41598-024-70014-4. Sci Rep. 2024. PMID: 39164334 Free PMC article.
-
Spike avalanches exhibit universal dynamics across the sleep-wake cycle.PLoS One. 2010 Nov 30;5(11):e14129. doi: 10.1371/journal.pone.0014129. PLoS One. 2010. PMID: 21152422 Free PMC article.
-
Self-organization and neuronal avalanches in networks of dissociated cortical neurons.Neuroscience. 2008 Jun 2;153(4):1354-69. doi: 10.1016/j.neuroscience.2008.03.050. Epub 2008 Mar 29. Neuroscience. 2008. PMID: 18448256
-
Coding properties of spiking neurons: reverse and cross-correlations.Neural Netw. 2001 Jul-Sep;14(6-7):599-610. doi: 10.1016/s0893-6080(01)00053-3. Neural Netw. 2001. PMID: 11665756 Review.
-
A new approach to spike sorting for multi-neuronal activities recorded with a tetrode--how ICA can be practical.Neurosci Res. 2003 Jul;46(3):265-72. doi: 10.1016/s0168-0102(03)00103-2. Neurosci Res. 2003. PMID: 12804787 Review.
Cited by
-
Modular architecture facilitates noise-driven control of synchrony in neuronal networks.Sci Adv. 2023 Aug 25;9(34):eade1755. doi: 10.1126/sciadv.ade1755. Epub 2023 Aug 25. Sci Adv. 2023. PMID: 37624893 Free PMC article.
-
Low-dimensional criticality embedded in high-dimensional awake brain dynamics.Sci Adv. 2024 Apr 26;10(17):eadj9303. doi: 10.1126/sciadv.adj9303. Epub 2024 Apr 26. Sci Adv. 2024. PMID: 38669340 Free PMC article.
-
Neuronal connected burst cascades bridge macroscale adaptive signatures across arousal states.Nat Commun. 2023 Oct 27;14(1):6846. doi: 10.1038/s41467-023-42465-2. Nat Commun. 2023. PMID: 37891167 Free PMC article.
-
Dissociated neuronal cultures as model systems for self-organized prediction.Front Neural Circuits. 2025 Jun 25;19:1568652. doi: 10.3389/fncir.2025.1568652. eCollection 2025. Front Neural Circuits. 2025. PMID: 40635884 Free PMC article. Review.
References
-
- Dunkelmann S, Radons G. Neural Networsk and Abelian Sandpile Models of Self-Organized Criticality. In: Marinaro M, Morasso PG, editors. Proceedings of International Conference Artificial Neural Networks. Springer-Verlag; 1994. p. 867–870.
-
- Muñoz MA. Colloquium: Criticality and dynamical scaling in living systems. Reviews of Modern Physics. 2018;90(3):031001. doi: 10.1103/RevModPhys.90.031001 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

