Computational approaches for network-based integrative multi-omics analysis

Abstract

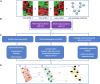
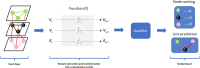
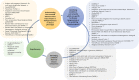
Advances in omics technologies allow for holistic studies into biological systems. These studies rely on integrative data analysis techniques to obtain a comprehensive view of the dynamics of cellular processes, and molecular mechanisms. Network-based integrative approaches have revolutionized multi-omics analysis by providing the framework to represent interactions between multiple different omics-layers in a graph, which may faithfully reflect the molecular wiring in a cell. Here we review network-based multi-omics/multi-modal integrative analytical approaches. We classify these approaches according to the type of omics data supported, the methods and/or algorithms implemented, their node and/or edge weighting components, and their ability to identify key nodes and subnetworks. We show how these approaches can be used to identify biomarkers, disease subtypes, crosstalk, causality, and molecular drivers of physiological and pathological mechanisms. We provide insight into the most appropriate methods and tools for research questions as showcased around the aetiology and treatment of COVID-19 that can be informed by multi-omics data integration. We conclude with an overview of challenges associated with multi-omics network-based analysis, such as reproducibility, heterogeneity, (biological) interpretability of the results, and we highlight some future directions for network-based integration.

Keywords: data integration; machine learning; multi-modal network; multi-omics; network causal inference; network diffusion/propagation.

FIGURE 1

An overview of the multi-omics integration approach and the methods for network-based integration. (A) Processed omics data and prior knowledge for integrative analysis. (B) An integrative multi-omics approach that could be implemented. (C) Integrative network-based methods (D) Multi-layered network showing intra-layer interaction (solid lines) and crosstalk (dashed lines) across different layers (L1, L2, L3). The nodes are shaped and coloured to represent different omics features within the omics layers they are involved in. The edges are coloured to show different interactions within and between omics layers.

FIGURE 2

Graph Neural Networks (GNNs) are a class of deep learning methods designed to perform inference and predictions on graph data by learning embeddings for graph attributes (nodes, edges, global-context). The concept behind the architecture of these methods is such that it accepts graph data as input and produces the same input graph with updated embeddings before making predictions. GNN uses a function (f) on each graph component vector [nodes vector (Vn), edge vector (En), global-context vector (Un)] in the input graph to learn abstract feature representations of the graph to compute a new feature vector for nodes (Vn+1), edges (En+1) and global-context (Un+1)). The output layer could predict nodes ranked according to a particular score (s1, s2, s3) and also predict edges (links) in the input network.

FIGURE 3

(A) Describes a random walk from the seed node (e.g., node A). The concept behind random walk is a guilt-by-association approach where an imaginary particle explores the network structure from seed nodes. The direction of movement of the particle is completely independent of the previous directions moved. At each step, the particle transition from any node in the graph with a certain probability (shown on the edges). The probability flow of random walks on a network is used as a proxy for information flows in the network to study the function of features, subnetworks, and prioritize features in the network. After several iterations, we are interested in the distribution of our position (Stationary distribution) in the graph (final state after iterative walks). The stationary probability distribution can be seen as a measure of the proximity between the seed(s) and all the other nodes in the graph. Nodes within the network can be prioritized using a specific metric (s1, s2, s3) such as the geometric mean of their proximity to seed nodes. (B) Describes heat diffusion from a reference query (e.g., node A). The concept behind heat diffusion in biological networks is perturbing nodes and simulating how the disturbance flows across edges within the network. Node disturbance means adding a scalar value (e.g., log fold changes from gene expression experiment, copy number variations) to node(s). Within a biological network, heat diffusion allows for the assessment of connectivity and topology of features which can allow the identification of relevant/dysregulated pathways and/or mutational effects across edges to neighbouring nodes. The purple arrow means diffusion jumps across different layers. The thickness of the purple arrow signifies the effect of query node (A) on nodes (F) and (H) as shown in nodes (F) and (H) in the final state graph after diffusion. Nodes within the network can be prioritized using a specific metric such as diffusion state distance.

FIGURE 4

Overview of the discussed network-based multi-omics integrative tools and research questions (in the circle) that they can be applied to. The tools implement different methods including unsupervised machine learning (*), supervised machine learning (**), neural networks (***), diffusion-based (+), random walk (++), differential network (#), probabilistic graphical model (##) and Bayesian methods (###).