Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022;31(4):1177-1188.
doi: 10.1080/10618600.2022.2069778. Epub 2022 May 26.

Bayesian Distance Weighted Discrimination

Eric F Lock  1
Affiliations

Bayesian Distance Weighted Discrimination

Eric F Lock. J Comput Graph Stat. 2022.

Abstract

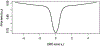
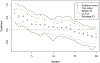
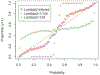
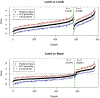
Distance weighted discrimination (DWD) is a linear discrimination method that is particularly well-suited for classification tasks with high-dimensional data. The DWD coefficients minimize an intuitive objective function, which can solved efficiently using state-of-the-art optimization techniques. However, DWD has not yet been cast into a model-based framework for statistical inference. In this article we show that DWD identifies the mode of a proper Bayesian posterior distribution, that results from a particular link function for the class probabilities and a shrinkage-inducing proper prior distribution on the coefficients. We describe a relatively efficient Markov chain Monte Carlo (MCMC) algorithm to simulate from the true posterior under this Bayesian framework. We show that the posterior is asymptotically normal and derive the mean and covariance matrix of its limiting distribution. Through several simulation studies and an application to breast cancer genomics we demonstrate how the Bayesian approach to DWD can be used to (1) compute well-calibrated posterior class probabilities, (2) assess uncertainty in the DWD coefficients and resulting sample scores, (3) improve power via semi-supervised analysis when not all class labels are available, and (4) automatically determine a penalty tuning parameter within the model-based framework. R code to perform Bayesian DWD is available at https://github.com/lockEF/BayesianDWD.

Keywords: Cancer genomics; distance weighted discrimination; high-dimensional data; probabilistic classification.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Class probability as a function of linear score under different links.
Fig. 2
Fig. 2
Prior term f(ui) (8) as a function of DWD score ui.
Fig. 3
Fig. 3
Inferential results and true values for the coefficients β for a dataset generated under the Uniform scenario when λ = 0.1, n = 100 and p = 20.
Fig. 4
Fig. 4
Estimated probabilities vs. observed proportions on test observations, aggregated across all conditions, for different simulation scenarios using the posterior mean or mode.
Fig. 5
Fig. 5
Different performance metrics (KL-divergence, test MSE, and test misclassification rate) are shown as a function of λ used for estimation under different conditions.
Fig. 6
Fig. 6
Estimated probabilities vs. observed proportions on test observations, aggregated across all conditions, for λ = 1 / 128, λ = 128, or inferring λ with a uniform prior.
Fig. 7
Fig. 7
Estimated probabilities vs. observed proportions on test observations, aggregated across all comparisons, using Bayesian DWD, random forests (RF), Bayesian SVM, and Bayesian logistic regression.
Fig. 8
Fig. 8
Mean DWD scores and associated 95% credible intervals for LumA vs. Basal and for LumA vs. LumB.
See this image and copyright information in PMC

References

    1. Breiman L (2001), ‘Random forests’, Machine learning 45(1), 5–32.
    1. Carlin BP and Louis TA (2008), Bayesian methods for data analysis, CRC Press.
    1. Cortes C and Vapnik V (1995), ‘Support-vector networks’, Machine learning 20(3), 273–297.
    1. Gelman A, Jakulin A, Pittau MG and Su Y-S (2008), ‘A weakly informative default prior distribution for logistic and other regression models’, The annals of applied statistics 2(4), 1360–1383.
    1. Ghosal S (1997), A review of consistency and convergence of posterior distribution, in ‘Varanashi Symposium in Bayesian Inference, Banaras Hindu University’.