Adaptive Design Optimization for a Mnemonic Similarity Task
- PMID: 36465949
- PMCID: PMC9718490
- DOI: 10.1016/j.jmp.2022.102665
Adaptive Design Optimization for a Mnemonic Similarity Task
Abstract
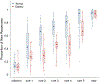
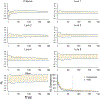
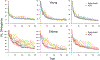
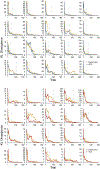
The Mnemonic Similarity Task (MST: Stark et al., 2019) is a modified recognition memory task designed to place strong demand on pattern separation. The sensitivity and reliability of the MST make it an extremely valuable tool in clinical settings, where it has been used to identify hippocampal dysfunction associated with healthy aging, dementia, schizophrenia, depression, and other disorders. As with any test used in a clinical setting, it is especially important for the MST to be administered as efficiently as possible. We apply adaptive design optimization methods (Lesmes et al., 2015; Myung et al., 2013) to optimize the presentation of test stimuli in accordance with previous responses. This optimization is based on a signal-detection model of an individual's memory capabilities and decision-making processes. We demonstrate that the adaptive design optimization approach generally reduces the number of test stimuli needed to provide these measures.
Keywords: Adaptive Design Optimization; Bayesian graphical models; Mnemonic Similarity Task; Signal Detection Theory; recognition memory.
Figures




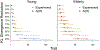



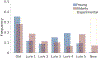
References
-
- Batchelder WH & Riefer DM (1980). Separation of Storage and Retrieval Factors in Free Recall of Clusterable Pairs. Psychological Review, 87, 375–397.
-
- Bröder A & Schiffer S (2006). Stimulus format and working memory in fast and frugal strategy selection. Journal of Behavioral Decision Making, 19, 361–380.
-
- Brown MW & Aggleton JP (2001). Recognition memory: what are the roles of the perirhinal cortex and hippocampus? Nature Reviews Neuroscience, 2, 51–61. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

