. 2022 Nov 22:1-12.

doi: 10.1007/s40435-022-01083-4. Online ahead of print.

Qualitative analysis of a fractional-order two-strain epidemic model with vaccination and general non-monotonic incidence rate

Mohamed Yasser Sahnoune^#¹, Adil Ez-Zetouni^#¹, Khadija Akdim^#¹, Mehdi Zahid^#¹

Affiliations

Affiliation

¹ Department of Mathematics, Faculty of Sciences and Technology, Cadi Ayyad University, PO Box 549, 40000 Marrakesh, Morocco.

^# Contributed equally.

PMID: 36465981
PMCID: PMC9685025
DOI: 10.1007/s40435-022-01083-4

Qualitative analysis of a fractional-order two-strain epidemic model with vaccination and general non-monotonic incidence rate

Mohamed Yasser Sahnoune et al. Int J Dyn Control. 2022.

. 2022 Nov 22:1-12.

doi: 10.1007/s40435-022-01083-4. Online ahead of print.

Authors

Mohamed Yasser Sahnoune^#¹, Adil Ez-Zetouni^#¹, Khadija Akdim^#¹, Mehdi Zahid^#¹

Affiliation

¹ Department of Mathematics, Faculty of Sciences and Technology, Cadi Ayyad University, PO Box 549, 40000 Marrakesh, Morocco.

^# Contributed equally.

PMID: 36465981
PMCID: PMC9685025
DOI: 10.1007/s40435-022-01083-4

Abstract

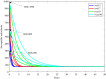
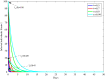
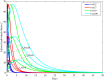
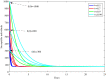
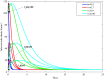
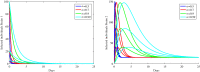
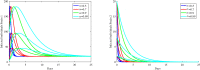
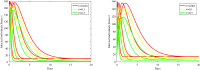
In this paper, a fractional-order two-strain epidemic model with vaccination and general non-monotonic incidence rate is analyzed. The studied problem is formulated using susceptible, infectious and recovered compartmental model. A Caputo fractional operator is incorporated in each compartment to describe the memory effect related to an epidemic evolution. First, the global existence, positivity and boundedness of solutions of the proposed model are proved. The basic reproduction numbers associated with studied problem are calculated. Four steady states are given, namely the disease-free equilibrium, the strain 1 endemic equilibrium, the strain 2 endemic equilibrium, and the endemic equilibrium associated with both strains. By considering appropriate Lyapunov functions, the global stability of the equilibrium points is proven according to the model parameters. Our modeling approach using a generalized non-monotonic incidence functions encloses a variety of fractional-order epidemic models existing in the literature. Finally, the theoretical findings are illustrated using numerical simulations.

Keywords: Caputo derivative; Global stability; Non-monotonic incidence function; Two-strain; Vaccination.

© The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature 2022, Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

PubMed Disclaimer

Conflict of interest statement

Conflict of interestThe authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in the above mentioned paper.

Figures

**Fig. 1**
Global behavior of susceptible population as function of time for $Λ = 7, μ = 0.08, ν = 0.01 ; β_{1} = 0.0015 ; β_{2} = 0.006 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different initial conditions $S (0) = 1000 ; 600 ; 300$ which corresponds to the stability of the disease-free equilibrium $E^{0}$

**Fig. 2**
Global behavior of strain 1 infection as function of time for $Λ = 7, μ = 0.08, ν = 0.01 ; β_{1} = 0.0015 ; β_{2} = 0.006 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different initial conditions $I_{1} (0) = 100 ; 20 ; 5$ which corresponds to the stability of the disease-free equilibrium $E^{0}$

**Fig. 3**
Global behavior of strain 2 infection as function of time for $Λ = 7, μ = 0.08, ν = 0.01 ; β_{1} = 0.0015 ; β_{2} = 0.006 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different initial conditions $I_{2} (0) = 20 ; 8 ; 2$ which corresponds to the stability of the disease-free equilibrium $E^{0}$

**Fig. 4**
Global behavior of susceptible population as function of time for $Λ = 17, μ = 0.08, ν = 0.01 ; β_{1} = 0.01 ; β_{2} = 0.015 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different initial conditions $S (0) = 1000 ; 600 ; 300$ which corresponds to the stability of the endemic equilibrium $E^{⋆}$

**Fig. 5**
Global behavior of susceptible population as function of time for $Λ = 17, μ = 0.08, ν = 0.01 ; β_{1} = 0.01 ; β_{2} = 0.015 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different initial conditions $I_{1} (0) = 100 ; 20 ; 5$ which corresponds to the stability of the endemic equilibrium $E^{⋆}$

**Fig. 6**
Global behavior of susceptible population as function of time for $Λ = 17, μ = 0.08, ν = 0.01 ; β_{1} = 0.01 ; β_{2} = 0.015 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different initial conditions $I_{2} (0) = 20 ; 8 ; 2$ which corresponds to the stability of the endemic equilibrium $E^{⋆}$

**Fig. 7**
Dynamics behavior of both strains infection (strain 1 (left), strain 2 (right)) as function of time for $Λ = 17, μ = 0.08, ν = 0.04 ; β_{1} = 0.004 ; β_{2} = 0.015 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.5 ; γ_{2} = 0.3 ; k_{1} = 0.4 ; k_{2} = 0.1$ and different initial conditions $I_{1} (0) = 100 ; 20 ; 5$ , $I_{2} (0) = 20 ; 8 ; 2$ and $S (0) = 1000 ; 600 ; 300$ which corresponds to the stability of the strain 2 endemic equilibrium $E^{2, ⋆}$

**Fig. 8**
Dynamics behavior of both strains infection (strain 1 (left), strain 2 (right)) as function of time for $Λ = 17, μ = 0.08, ν = 0.01 ; β_{1} = 0.015 ; β_{2} = 0.0015 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.3 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.4$ and different initial conditions $I_{1} (0) = 100 ; 20 ; 5$ , $I_{2} (0) = 20 ; 8 ; 2$ and $S (0) = 1000 ; 600 ; 300$ which corresponds to the stability of the strain 1 endemic equilibrium $E^{1, ⋆}$

**Fig. 9**
Simulation of the vaccine impact on the behavior of the infection starting from initial condition $(S (0), I_{1} (0), I_{2} (0)) = (1000, 100, 20)$ and for parameter values $Λ = 17, μ = 0.08, ν = 0.01 ; β_{1} = 0.02 ; β_{2} = 0.02 ; d_{1} = 0.1 ; d_{2} = 0.1 ; γ_{1} = 0.4 ; γ_{2} = 0.3 ; k_{1} = 0.1 ; k_{2} = 0.1$ and different fractional parameters order $α = 1 ; 0.9 ; 0.7 ; 0.5$

See this image and copyright information in PMC

References

1. Podlubny I (1999) Fractional differential equations. Maths Sci. Eng, San Diego
1. Huo J, Zhao H, Zhu L. The effect of vaccines on backward bifurcation in a fractional order HIV model. Nonlinear Anal Real World Appl. 2015;26:289–305. doi: 10.1016/j.nonrwa.2015.05.014. - DOI
1. Khan MA, Atagana A. Modelling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex Eng J. 2020;59(4):2379–2389. doi: 10.1016/j.aej.2020.02.033. - DOI
1. Petráš I. Fractional-order nonlinear systems: modeling, analysis and simulation. Berlin: Springer Science & Business Media; 2011.
1. Ahmed E, El-Sayed A, El-Saka HA. On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys Lett A. 2006;358(1):1–4. doi: 10.1016/j.physleta.2006.0.087. - DOI

LinkOut - more resources

Full Text Sources
- Europe PubMed Central
- PubMed Central

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Qualitative analysis of a fractional-order two-strain epidemic model with vaccination and general non-monotonic incidence rate

Affiliation

Qualitative analysis of a fractional-order two-strain epidemic model with vaccination and general non-monotonic incidence rate

Authors

Affiliation

Abstract

Conflict of interest statement

Figures

Similar articles

References

LinkOut - more resources

Full Text Sources