High-fidelity qutrit entangling gates for superconducting circuits

Abstract

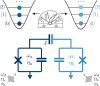
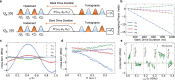
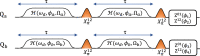
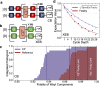
Ternary quantum information processing in superconducting devices poses a promising alternative to its more popular binary counterpart through larger, more connected computational spaces and proposed advantages in quantum simulation and error correction. Although generally operated as qubits, transmons have readily addressable higher levels, making them natural candidates for operation as quantum three-level systems (qutrits). Recent works in transmon devices have realized high fidelity single qutrit operation. Nonetheless, effectively engineering a high-fidelity two-qutrit entanglement remains a central challenge for realizing qutrit processing in a transmon device. In this work, we apply the differential AC Stark shift to implement a flexible, microwave-activated, and dynamic cross-Kerr entanglement between two fixed-frequency transmon qutrits, expanding on work performed for the ZZ interaction with transmon qubits. We then use this interaction to engineer efficient, high-fidelity qutrit CZ^† and CZ gates, with estimated process fidelities of 97.3(1)% and 95.2(3)% respectively, a significant step forward for operating qutrits on a multi-transmon device.

Fig. 1. Microwave-activated cross-Kerr entanglement.

Two transmon qutrits with qubit frequency ω_i, anharmonicity η_i, and coupling J, experience a dynamical cross-Kerr (ZZ-like) entanglement when simultaneously driven by an off-resonant microwave drive. The strength of the cross-Kerr entangling terms (α₁₁, α₁₂, α₂₁, α₂₂) is tuned by the parameters of the microwave drive (ω_d, Ω, ϕ).

Fig. 2. Characterizing the dynamical cross-Kerr entanglement.

a To study the accumulation of entangling phases under the driven cross-Kerr interaction, we place two qutrits in a full superposition using ternary Hadamard gates (virtual Z gates ommited in diagram), then study the evolution under the Stark drive scheme by performing state tomography. b We demonstrate fitting the accumulation of entangling phase found by tomography to our linear, driven cross-Kerr model, where α_ij is the slope of the line and the uncertainty is from the linear fit. c, d, We match the behavior of the cross-Kerr entanglement given relevant experimental parameters in our system to our Hamiltonian model for the relative phase of the driving, ϕ, and amplitude of the driving, fixing Ω = Ω_a = Ω_b. e We additionally compare the dependence of α₁₂ on the frequency of the drive ω_d using an ab-initio master equation simulation in QuTiP^,.

Fig. 3. Gate schematic.

For the CZ and CZ^† gate, we perform two rounds of cross-Kerr entanglement for duration τ with interleaved echo pulses in the $\left\{∣1⟩,∣2⟩\right\}$ subspace which shuffle the entangling phases. For proper conditions on the α_ij terms in Eq. (1), the CZ^†(CZ) is compiled with a total gate time of 580(783) ns. The local Z terms in both two level subspaces of the qutrit are then undone using virtual Z gates.

Fig. 4. Benchmarking.

a Circuit schematic of cycle benchmarking (CB). The errors of the CZ^† are twirled via random Weyl gates (red) to tailor errors into stochastic Weyl channels. The initial state and measurement basis (blue) are selected to pick out the decay associated with specific Weyl channels. b Circuit schematic of cross-entropy benchmarking (XEB). The errors of the CZ^† are twirled via random SU(3) gates (green) to tailor the noise to a simple depolarizing channel. c An integrated histogram of CB for both the CZ^† gate and a reference cycle, with the solid vertical lines giving the fidelities 0.936(1) and 0.966(1) respectively, yielding an estimated process fidelity of 97.3(1)%. We extract an error budget directly from CB, estimating a purity limited fidelity of 0.973(9) and 0.989 (with negligible error) for the dressed CZ^† and reference cycles, yielding a purity limit 0.986(9) for the isolated CZ^† gate. d From XEB we estimate the depolarized fidelity as 0.933(3). Additionally, we estimate the speckle-purity limited fidelity of the CZ^† dressed with random SU(3) gates to be 0.961(3).

Fig. 5. Demonstration of gate expressability.

a A parameterized Ansatz circuit (V) is used to synthesize a target unitary (U), given some 2-qutrit gate and arbitrary SU(3) gates. b We study the Ansatz circuit (V) for the different two-qutrit gates discussed in the text for 1000 Haar random and Clifford gates, minimizing the infidelity $1-\mathcal{F}$(V,U). The dashed lines represent 100% numerical success for synthesizing our set of Haar random gates, and the bars display the success rate for synthesizing Clifford gates. We perform the minimization until we find a 100% success rate for each two-qutrit gate between depths 0 ≤ m ≤ 9. c An experimentally reconstructed density matrix of the two qutrit Bell state $∣\psi ⟩=\frac{1}{\sqrt{3}}\left(∣00⟩+∣11⟩+∣22⟩\right)$ formed using a single CZ gate with state fidelity $\mathcal{F}=0.952$. The black outline is the target density matrix.