The tree of blobs of a species network: identifiability under the coalescent

Abstract

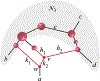
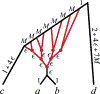
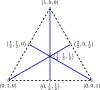
Inference of species networks from genomic data under the Network Multispecies Coalescent Model is currently severely limited by heavy computational demands. It also remains unclear how complicated networks can be for consistent inference to be possible. As a step toward inferring a general species network, this work considers its tree of blobs, in which non-cut edges are contracted to nodes, so only tree-like relationships between the taxa are shown. An identifiability theorem, that most features of the unrooted tree of blobs can be determined from the distribution of gene quartet topologies, is established. This depends upon an analysis of gene quartet concordance factors under the model, together with a new combinatorial inference rule. The arguments for this theoretical result suggest a practical algorithm for tree of blobs inference, to be fully developed in a subsequent work.

Keywords: Network multispecies coalescent model; Phylogenetics; Phylogenomics; Species network; Tree of blobs.

Fig. 1

LA species network 𝒩⁺, with edge lengths in coalescent units. Red indicates hybrid nodes and hybrid edges. The lowest stable ancestor (LSA) of the network is v. This network has 6 non-trivial blobs (a 5-blob, two 3-blobs, and three 2-blobs), and a single trivial 3-blob. C The tree-like structure of the LSA network 𝒩^⊕, obtained by deleting parts of the network above the LSA v, and showing blobs as red spheres. A sphere is used to suggest an unknown and potentially complicated blob structure. R The reduced unrooted tree of blobs, T_rd (𝒩⁻), obtained by shrinking blobs in the LSA network to nodes, unrooting, and suppressing degree-2 nodes

Fig. 2

Examples of blobs in networks. Red indicates hybrid nodes, and hybrid edges above them. Cut edges incident to the blobs are represented by dotted line segments: L a planar 5-blob, C a non-planar 4-blob, R a single 2-blob in a non-binary network, formed from two 2-cycles sharing a single node

Fig. 3

A network with a 5-blob determined by the sets {a, b, c}, {a, b, d, f}, and other sets. The set {a, b, e, f}, however, does not determine a blob. Both {a, b, c, d} and {a, b, d, e} are B-quartets on this network. While {a, b, c, d} is also a B-quartet on its induced 4-taxon network, {a, b, d, e} is a T-quartet on its induced 4-taxon network

Fig. 4

L Schematic depictions of two semidirected unrooted 4-taxon networks 𝒩⁻, where spheres represent blobs of unspecified structure, and R their reduced unrooted trees of blobs T_rd (𝒩⁻). Up to taxon labelling, these are the only possible 4-taxon topological reduced unrooted trees of blobs

Fig. 5

The schematic form of the 4-taxon network 𝒩⁺ used to establish Claim (b) in the proof of Theorem 1. The root (unlabelled) could be anywhere in the gray region. Red spheres represent biconnected subgraphs, which may become blobs on induced networks on subsets of taxa. With w the lowest hybrid node in 𝒩⁺, one of its hybrid edges, k₁, is removed since doing so leaves a 4-blob. With v then the lowest hybrid node, removing either of its hybrid edges, h₁, h₂, would result in no 4-blob. We let ${𝒩}_1^{+}$ be the result of further removing edge h₂ and edges ancestral to it and only the taxon a. The network ${𝒩}_2^{+}$ results similarly from further removing edge h₁ instead of h₂. Removing all edges and nodes which lie above only the taxon a gives network N₃, shown in the gray region. The edge e is the cut edge incident to the single 3-blob in N₃, through which paths from that blob to taxon b pass

Fig. 6

An instance of the network 𝒩(k)⁺ used in the proof of Proposition 1, with k = 3. All hybridization parameters are 1/2, while ϵ and M denote variable edge lengths

Fig. 7

Geometric view of CFs for 4-taxon network models, with dashed lines outlining the simplex Δ². The solid line segments represent CFs arising from species networks whose unrooted reduced trees of blobs are resolved. The vertical line segment corresponds to ab|cd, the upward-sloping one to ac|bd, and the downward sloping one to ad|bc. CFs off of these lines can only arise from networks with unresolved unrooted reduced trees of blobs, and as shown in Baños (2019) all such points arise from level-1 networks. Networks whose unrooted reduced trees of blobs are unresolved may also produce CFs on the line segments, but only for non-generic parameters

Fig. 8

A schematic of the network 𝒩⁺, as described in Lemma 3. Edges are partitioned into four color-coded sets. Black edges are ancestral to the taxon α and no other taxa, forming the subnetwork A. Non-black edges form the subnetwork 𝒩′, in which the blob ℬ′ is determined by {a, b, c}. The red edge e₀ incident to ℬ′ is a cut edge of 𝒩′, separating the connected components K_ab and K_cd, shown in green and blue, respectively. The root of 𝒩⁺ might be in either K_ab or K_cd. The nodes x, y, z are described in the proof of the lemma

Fig. 9

L A 7-blob with a simple cycle structure. While many of its B-quartets are not CF-detectable, each can be inferred from CF-detectable ones by a single application of the B-quartet Inference Rule. For instance, {a, b, c, d} is a B-quartet although CF_abcd is ad|bc-cut. The inference rule shows that it is a B-quartet using the two CF-detectable ones, {α, a, c, d} and {α, b, c, d}. R A 7-blob with a more complex structure. The B-quartet {a, b, c, d} is not CF-detectable, but three applications of the inference rule allow it to be inferred from those that are