Optical-cavity mode squeezing by free electrons

Abstract

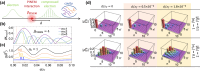
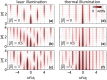
The generation of nonclassical light states bears a paramount importance in quantum optics and is largely relying on the interaction between intense laser pulses and nonlinear media. Recently, electron beams, such as those used in ultrafast electron microscopy to retrieve information from a specimen, have been proposed as a tool to manipulate both bright and dark confined optical excitations, inducing semiclassical states of light that range from coherent to thermal mixtures. Here, we show that the ponderomotive contribution to the electron-cavity interaction, which we argue to be significant for low-energy electrons subject to strongly confined near-fields, can actually create a more general set of optical states, including coherent and squeezed states. The postinteraction electron spectrum further reveals signatures of the nontrivial role played by A ² terms in the light-matter coupling Hamiltonian, particularly when the cavity is previously excited by either chaotic or coherent illumination. Our work introduces a disruptive approach to the creation of nontrivial quantum cavity states for quantum information and optics applications, while it suggests unexplored possibilities for electron beam shaping.

Keywords: light–matter interaction; ponderomotive interaction; quantum optics; squeezed states.

Figure 1:

Free-electron interaction with an optical cavity. We present a sketch of the interaction for a single-mode cavity. Both linear (∝ v · A) and quadratic (ponderomotive ∝ A ²) terms in the quantum vector potential operator A are present in the minimal-coupling light–matter interaction Hamiltonian. Switching on and off these two terms selects the creation of either coherent or squeezed cavity mode states, respectively.

Figure 2:

Linear and quadratic coupling in phase-matched interactions. (a) Deviation of the linear coupling coefficient $|{\tilde{\beta }}_0|$ from the value obtained by neglecting the ponderomotive force |β ₀| as a function of |σ ₀| for a phase-matched interaction with real η _i [see Eqs. (3) and (8a)]. (b) Squeezing parameter |σ ₀| (left vertical axis) and squeezing factor 20|σ ₀| dB (right vertical axis) as a function of η = ω ₀ a/v for different values of v ² a under the electron–cavity configuration depicted in the inset, in which the e-beam moves with velocity v along the axis of a cylindrical hole of radius a and the cavity mode consists of a polariton made of a combination of azimuthal numbers m = ±1 and phase-matched axial wave vector q _z = ω ₀/v.

Figure 3:

Postinteraction cavity-mode population. (a) Sketch of an electron wave packet undergoing a classical PINEM interaction of strength β _PINEM, and subsequently propagating in free-space for a distance d, where it develops a sequence of probability-density pulses and interacts with a cavity with coupling coefficients σ ₀ and ${\tilde{\beta }}_0$ . (b) Coherence factor $|M_{m{\omega }_0/v}|$ , determining the amount of coherence left in the two-photon coherent state [see Eq. (9a)] for the scenario depicted in panel (a) with β _PINEM = 4. We plot the result as a function of the normalized propagation distance d/z _T for several harmonics m. (c) Position variance $⟨\mathrm{\Delta }{\widehat{X}}^2⟩$ for a PINEM-compressed electron [solid curves; see panel (a)] and for a perfectly coherent electron (dashed curves). We consider different real values of σ ₀ with $\tilde{\beta }=0$ , θ _n = 0, and λ = 0. (d) Elements ${\rho }_{n{n}^{\prime }}^{\text{ph}}$ of the density matrix associated with the cavity state after interaction with a compressed electron [see panel (a)]. The interaction region is taken to be placed at the propagation distances highlighted by the color-coordinated vertical dashed lines in panel (b) assuming pairs of coupling parameters $|{\tilde{\beta }}_0|=0.1$ and |σ ₀| = 1 (top row); or $|{\tilde{\beta }}_0|=2$ , |σ ₀| = 0.1 (bottom row). All plots in panel (d) are calculated for ϕ = 0.

Figure 4:

Electron energy-loss spectrum. Electron distribution as a function of the normalized energy loss ω/ω ₀ and the ponderomotive coupling |σ| for $|\tilde{\beta }|=0$ (a, d), $|\tilde{\beta }|=0.5$ (b, e), and $|\tilde{\beta }|=1$ (c, f). We take the cavity to be initially prepared in either a coherent state (a–c) or a thermal state (d–f), as described by Eqs. (13) or (14), respectively. The conditions $\overline{n}\gg 1$ and ϕ = π/2 are assumed in all panels, and a Lorentzian broadening in ω (FWHM = 0.12ω ₀) is introduced for clarity.