CRYSTAL23: A Program for Computational Solid State Physics and Chemistry
- PMID: 36502394
- PMCID: PMC10601489
- DOI: 10.1021/acs.jctc.2c00958
CRYSTAL23: A Program for Computational Solid State Physics and Chemistry
Abstract
The Crystal program for quantum-mechanical simulations of materials has been bridging the realm of molecular quantum chemistry to the realm of solid state physics for many years, since its first public version released back in 1988. This peculiarity stems from the use of atom-centered basis functions within a linear combination of atomic orbitals (LCAO) approach and from the corresponding efficiency in the evaluation of the exact Fock exchange series. In particular, this has led to the implementation of a rich variety of hybrid density functional approximations since 1998. Nowadays, it is acknowledged by a broad community of solid state chemists and physicists that the inclusion of a fraction of Fock exchange in the exchange-correlation potential of the density functional theory is key to a better description of many properties of materials (electronic, magnetic, mechanical, spintronic, lattice-dynamical, etc.). Here, the main developments made to the program in the last five years (i.e., since the previous release, Crystal17) are presented and some of their most noteworthy applications reviewed.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
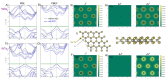

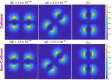
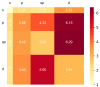
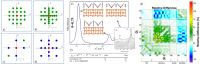
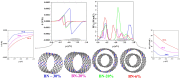
 , while the arrow length and direction represent
the in-plane components mx and mz.
, while the arrow length and direction represent
the in-plane components mx and mz.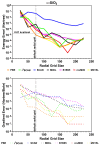





References
-
- Hafner J.; Kresse G.. Properties of Complex Inorganic Solids; Springer, 1997; pp 69–82.
Publication types
LinkOut - more resources
Full Text Sources

