Dynamics of a fractional order mathematical model for COVID-19 epidemic transmission

Abstract

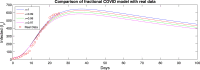
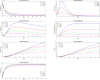
To achieve the aim of immediately halting spread of COVID-19 it is essential to know the dynamic behavior of the virus of intensive level of replication. Simply analyzing experimental data to learn about this disease consumes a lot of effort and cost. Mathematical models may be able to assist in this regard. Through integrating the mathematical frameworks with the accessible disease data it will be useful and outlay to comprehend the primary components involved in the spreading of COVID-19. There are so many techniques to formulate the impact of disease on the population mathematically, including deterministic modeling, stochastic modeling or fractional order modeling etc. Fractional derivative modeling is one of the essential techniques for analyzing real-world issues and making accurate assessments of situations. In this paper, a fractional order epidemic model that represents the transmission of COVID-19 using seven compartments of population susceptible, exposed, infective, recovered, the quarantine population, recovered-exposed, and dead population is provided. The fractional order derivative is considered in the Caputo sense. In order to determine the epidemic forecast and persistence, we calculate the reproduction number $R_0$ . Applying fixed point theory, the existence and uniqueness of the solutions of fractional order derivative have been studied . Moreover, we implement the generalized Adams-Bashforth-Moulton method to get an approximate solution of the fractional-order COVID-19 model. Finally, numerical result and an outstanding graphic simulation are presented.

Keywords: Adams–Bashforth Moulton method; COVID-19 model; Existence and uniqueness; Fractional calculus; Stability analysis.

Fig. 1

Comparison of simulation curves and real date on different fractional order for infected population.

Fig. 2

Simulations curves of COVID model governed by Caputo fractional operator and initial condition $(10999782,200,18,0,0,0,0)$.