Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Dec 2:16:1049985.
doi: 10.3389/fnhum.2022.1049985. eCollection 2022.

Tangent space alignment: Transfer learning for Brain-Computer Interface

Alexandre Bleuzé  1 , Jérémie Mattout  2 , Marco Congedo  1
Affiliations

Tangent space alignment: Transfer learning for Brain-Computer Interface

Alexandre Bleuzé et al. Front Hum Neurosci. .

Abstract

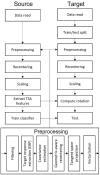
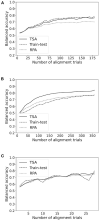
Statistical variability of electroencephalography (EEG) between subjects and between sessions is a common problem faced in the field of Brain-Computer Interface (BCI). Such variability prevents the usage of pre-trained machine learning models and requires the use of a calibration for every new session. This paper presents a new transfer learning (TL) method that deals with this variability. This method aims to reduce calibration time and even improve accuracy of BCI systems by aligning EEG data from one subject to the other in the tangent space of the positive definite matrices Riemannian manifold. We tested the method on 18 BCI databases comprising a total of 349 subjects pertaining to three BCI paradigms, namely, event related potentials (ERP), motor imagery (MI), and steady state visually evoked potentials (SSVEP). We employ a support vector classifier for feature classification. The results demonstrate a significant improvement of classification accuracy, as compared to a classical training-test pipeline, in the case of the ERP paradigm, whereas for both the MI and SSVEP paradigm no deterioration of performance is observed. A global 2.7% accuracy improvement is obtained compared to a previously published Riemannian method, Riemannian Procrustes Analysis (RPA). Interestingly, tangent space alignment has an intrinsic ability to deal with transfer learning for sets of data that have different number of channels, naturally applying to inter-dataset transfer learning.

Keywords: Brain-Computer Interface; ERP; Riemannian geometry; SSVEP; domain adaptation; motor imagery; transfer learning.

PubMed Disclaimer

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Figures

Figure 1
Figure 1
Flowchart summarizing the analysis pipeline.
Figure 2
Figure 2
Schematic of a two-class dataset using the first dimension of a PCA for each class.
Figure 3
Figure 3
Representative seriation plots for TSA (left) and RPA (right) methods for each paradigms. See text for details. (A) Database Cho2017 (MI). (B) Database brain invaders 2013a (ERP). (C) Database SSVEP exoskeleton (SSVEP).
Figure 4
Figure 4
Accuracy as a function of the number of alignment trials for TSA and RPA methods for a representative database in each paradigm (MI, ERP, SSVEP). (A) Database Cho2017 (MI). (B) Database brain invaders 2013a (ERP). (C) Database SSVEP exoskeleton (SSVEP).
Figure 5
Figure 5
Bar graph giving the inter-session balanced accuracy for the databases possessing multiple sessions.
See this image and copyright information in PMC

References

    1. Barachant A., Bonnet S., Congedo M., Jutten C. (2012). Multiclass brain-computer interface classification by Riemannian geometry. IEEE Trans. Biomed. Eng. 59, 920–928. 10.1109/TBME.2011.2172210 - DOI - PubMed
    1. Barachant A., Bonnet S., Congedo M., Jutten C. (2013). Classification of covariance matrices using a Riemannian-based kernel for BCI applications. Neurocomputing 2013, 172–178. 10.1016/j.neucom.2012.12.039 - DOI
    1. Barachant A., Bonnet S., Congedo M., Jutten C., Riemannian C. J., Bonnet S. (2010). Riemannian geometry applied to BCI classification. Lecture Notes Comput. Sci. 6365, 629–636. 10.1007/978-3-642-15995-4_78 - DOI
    1. Bhatia R. (2009). Positive Definite Matrices. Princeton, NJ: Princeton University Press. 10.1515/9781400827787 - DOI
    1. Bhatia R., Jain T., Lim Y. (2019). On the Bures-Wasserstein distance between positive definite matrices. Exposit. Math. 37, 165–191. 10.1016/j.exmath.2018.01.002 - DOI

LinkOut - more resources