Quasicriticality explains variability of human neural dynamics across life span

Abstract

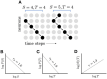
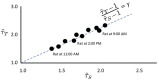
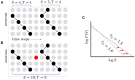
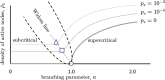
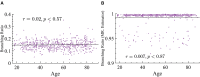
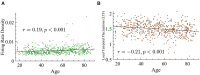
Aging impacts the brain's structural and functional organization and over time leads to various disorders, such as Alzheimer's disease and cognitive impairment. The process also impacts sensory function, bringing about a general slowing in various perceptual and cognitive functions. Here, we analyze the Cambridge Centre for Ageing and Neuroscience (Cam-CAN) resting-state magnetoencephalography (MEG) dataset-the largest aging cohort available-in light of the quasicriticality framework, a novel organizing principle for brain functionality which relates information processing and scaling properties of brain activity to brain connectivity and stimulus. Examination of the data using this framework reveals interesting correlations with age and gender of test subjects. Using simulated data as verification, our results suggest a link between changes to brain connectivity due to aging and increased dynamical fluctuations of neuronal firing rates. Our findings suggest a platform to develop biomarkers of neurological health.

Keywords: Cam-CAN dataset; aging; healthy human; magnetoencephalography (MEG); neuronal avalanches; quasicriticality.

Figure 1

Neuronal avalanches and their distributions. (A) Schematic network of five neurons; inactive neurons are represented by gray dots and active neurons by black dots; and propagation of activity is represented by arrows. Two avalanches are shown: the first with size 4 and duration 4, and the second with size 5 and duration 4. (B) In a critical network, the distribution of avalanche sizes S, follows a power law, which appears linear when plotted with logarithmic scales. The slope of this line gives the exponent τ_S = 1.6. (C) The distribution of avalanche durations, T, follows another power law with exponent τ_T = 1.8. (D) The average avalanche size for a given duration, 〈S〉(T), follows a power law with exponent γ = 4/3. The appearance of multiple power laws and the relationship between their exponents, (τ_T−1)/(τ_S−1) = γ, indicate that the network may be operating near a critical point.

Figure 2

Empirical data stay near the γ-scaling line. Depiction of avalanche duration exponents, ${\tilde{\tau }}_T$, plotted against avalanche size exponents, ${\tilde{\tau }}_S$ for data collected from the same rat at different times (similar to data presented by Fontenele et al., 2019). Note that in all cases, exponents lie close to the dashed γ-scaling line given by $\gamma =({\tilde{\tau }}_T-1)/({\tilde{\tau }}_S-1)$. Proximity to the γ-scaling line indicates closeness to the critical point.

Figure 3

How spontaneous activity reduces exponent magnitude. (A) Two avalanches as shown before. Note gap in activity separating them. (B) Spontaneous activity turns on neurons that would otherwise have been inactive (red circle), filling the gap. The two previously distinct avalanches are now merged together into a larger and longer avalanche. (C) The increase in large avalanches causes the tail of the distribution to move further to the right. This in turn causes the magnitude of the exponent ${\tilde{\tau }}_S$ to decrease (1.6–1.4). The figure illustrates schematically the results of quasicritical simulations (Fosque et al., 2021).

Figure 4

(A) Moving along the γ-scaling line. Avalanche duration exponents, ${\tilde{\tau }}_T$, plotted against avalanche size exponents, ${\tilde{\tau }}_S$ for different values of p_s. Note that in all cases, exponents lie close to the dashed γ-scaling line given by the equation $\gamma =({\tilde{\tau }}_T-1)/({\tilde{\tau }}_S-1)$. When there is no spontaneous activity, the magnitude of the exponents is largest (circle). As p_s is increased, the magnitude of the exponents decreases (square, then triangle). Schematic plot here summarizes results reported by Shew et al. (2015), Fontenele et al. (2019), and Fosque et al. (2021), and predicted by models of quasicriticality (Williams-Garćıa et al., ; Fosque et al., 2021). (B) Susceptibility, χ, is blunted by increases in p_s. When p_s = 0 and the branching parameter is exactly one, the susceptibility curve will diverge to infinity (circle). As p_s is increased (square, triangle), the susceptibility declines. Note that the branching parameter at which these curves peak also declines. This figure schematically depicts the predictions of a quasicritical network model (Williams-Garćıa et al., 2014) that have recently been corroborated with data from spiking networks (Fosque et al., 2021).

Figure 5

Phase diagram illustrating quasicriticality and the Widom line. When p_s = 0, there is an inactive phase to the left of the critical point (κ = 1 = σ) and an active phase to the right of it. The critical point is given by the circle. The thick gray curve shows how the fraction of active neurons (y-axis) varies as the control parameter κ is increased. As p_s is increased (lighter gray curves), this curve is shifted vertically and to the left. The points at which susceptibility will be maximal for each value of p_s are given by the square and the circle. While the network will not be critical at these points, it will be quasicritical (quasicritical region is enclosed with a parabolic black dashed line). This means that susceptibility will be maximal for that level of spontaneous activity. The dashed line joining these optimal points is called the Widom line. Note that the branching parameters at which maximum susceptibility occurs are now shifted to the left. We can also see that there are three main regions divided by the Widom line, the subcritical and supercritical ones. This figure schematically depicts predictions of a quasicritical network model (Williams-Garćıa et al., 2014) which have recently been corroborated with data from spiking networks (Fosque et al., 2021).

Figure 6

Pairs of size and duration effective exponents for each subject are transformed to a normalized value between 0 and 1. We call this measure the “position on the γ-scaling line.” This measure is obtained by (A) shifting the γ-scaling line, and (B) projecting each subject's duration-size vector onto the shifted γ-scaling line. The largest projection represents the value of 1.

Figure 7

Human data suggests that exponential decay of connection strengths becomes steeper with age. Figure adapted from Otte et al. (2015). Note that oldest age group (bottom) shows the sharpest drop, while the youngest age group (top) has the shallowest curve. For details, see text.

Figure 8

MEG data from 566 human subjects on the γ-scaling line with ages ranging from 18 to 88 years old. Error bars are shown in blue. A least-squares fit of exponent pairs is also shown in dashed line, and gives a least-squares fit of γ_lsf = 1.24 ± 0.02. Solid line indicates the average scaling slope, $\langle \frac{{\tilde{\tau }}_T-1}{{\tilde{\tau }}_S-1}\rangle =1.4\pm 0.4$. The scaling slope is the average of scaling fraction across subjects.

Figure 9

Older subjects display smaller exponents and higher susceptibility. (A) Older subjects have exponents that fall lower on the γ-scaling line. We found that there is a significant negative correlation between age and the magnitude of time and size exponents in our dataset. (B) Older subjects have higher dynamical susceptibility. There is a significant correlation between age and susceptibility.

Figure 10

There is a negative correlation between position on the line and susceptibility. This correlation suggests that subjects with smaller exponents have higher susceptibility (correlation r = −0.87, p < 0.001).

Figure 11

Variance of the avalanche size, var(S), for each individual; orange indicates the youngest half and blue the oldest half. (A) var(S) as a function of the age of individuals. We find a correlation with age of r = 0.213 with p < 0.001 in the log-linear scale. (B) var(S) vs. susceptibility, χ, for each subject. We find a correlation with susceptibility of r = 0.8449 with p < 0.001 in the log-linear scale.

Figure 12

Branching ratio does not significantly change with age. (A) Naive method: r = 0.02, p≈0.57. (B) MR. Estimator : r = −0.007, p≈0.87.

Figure 13

Age positively correlates with firing rate density and shows a negative correlation with LTF. (A) Firing rate density vs. age shows a significant positive correlation (r = 0.19, p < 0.001). The statistical significance of this relationship is not dependent on the three outlier values that are above 0.015. (B) LTF vs. age shows a significant negative correlation (r = −0.21, p < 0.001).

Figure 14

There is a small but statistically significant difference in position on the line between male and female subjects. The box plot shows the distribution of the female and male subjects' data and where they land on the line. For female subjects (mean = 0.64, SD = 0.10), while for male subjects (mean = 0.66, SD = 0.09). The two-tailed t-test gives t = −2.97 and p < 0.01 (indicated by the two stars).

Figure 15

Simulation on the γ-scaling line. Probability of spontaneous activation $p_s=10^{-3}$, and bias parameter B = 0.6 (red diamonds) and B = 1.8 (blue circles). The three points for each bias represent three different κ values around the peak of maximum susceptibility taken from Tables 1, 2. We can see that as we increase the bias parameter, the exponents get smaller while increasing susceptibility.