Dynamics and Equilibration Mechanisms in Block Copolymer Particles

Abstract

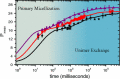
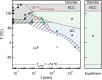
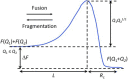
Self-assembly of block copolymers into interesting and useful nanostructures, in both solution and bulk, is a vibrant research arena. While much attention has been paid to characterization and prediction of equilibrium phases, the associated dynamic processes are far from fully understood. Here, we explore what is known and not known about the equilibration of particle phases in the bulk, and spherical micelles in solution. The presumed primary equilibration mechanisms are chain exchange, fusion, and fragmentation. These processes have been extensively studied in surfactants and lipids, where they occur on subsecond time scales. In contrast, increased chain lengths in block copolymers create much larger barriers, and time scales can become prohibitively slow. In practice, equilibration of block copolymers is achievable only in proximity to the critical micelle temperature (in solution) or the order-disorder transition (in the bulk). Detailed theories for these processes in block copolymers are few. In the bulk, the rate of chain exchange can be quantified by tracer diffusion measurements. Often the rate of equilibration, in terms of number density and aggregation number of particles, is much slower than chain exchange, and consequently observed particle phases are often metastable. This is particularly true in regions of the phase diagram where Frank-Kasper phases occur. Chain exchange in solution has been explored quantitatively by time-resolved SANS, but the results are not well captured by theory. Computer simulations, particularly via dissipative particle dynamics, are beginning to shed light on the chain escape mechanism at the molecular level. The rate of fragmentation has been quantified in a few experimental systems, and TEM images support a mechanism akin to the anaphase stage of mitosis in cells, via a thin neck that pinches off to produce two smaller micelles. Direct measurements of micelle fusion are quite rare. Suggestions for future theoretical, computational, and experimental efforts are offered.

Figure 1

Schematic representation of known packings of nominally spherical particles of BCPs in the bulk. These include the most prevalent body-centered cubic (BCC) and two close-packed phases: face-centered cubic (FCC) and hexagonally close-packed (HCP). In these three phases, all particles are equivalent. In the σ, A15, C14, and C15, phases, however, there are 5, 2, 3, and 2 distinct particle sizes, respectively, as indicated by the shaded Wigner–Seitz cells.

Figure 2

Schematic cartoon of five equilibration processes discussed in the text

Figure 3

Time dependence of the mean aggregation number, P_mean, detailing the two-step nature of the formation of micelles, reproduced with permission from ref (49). Copyright 2009 American Physical Society.

Figure 4

Primary peak position from SAXS measurements of 15% perdeuterated PS-PI (15–15) in tetradecane (lower trace), and 25% PS-perdeuterated PI (15–15) in diethyl phthalate (upper trace) versus temperature. Both solutions transition from a disordered solution of micelles to a BCC phase, and then to an FCC packing; the monotonic decrease in q* reflects increasing segregation and growth of micelle aggregation number, Q, with cooling in these UCMT systems. However, both systems depart from equilibrium near 50 °C. Reproduced with permission from ref (55). Copyright 2009 American Physical Society.

Figure 5

Tracer diffusion (D) of sphere-forming diblock copolymers in the melt, normalized to the diffusivity in the absence of structure (D₀), as a function of χ times the degree of polymerization of the core-forming block: (a) PEP–PDMS. Reproduced with permission from ref (66). Copyright 2003 American Chemical Society. (b) PS-P2VP. Reproduced with permission from ref (62). Copyright 1998 American Chemical Society. The straight line in each panel is the same, indicating the quantitative equivalence of the results.

Figure 6

(a) Primary peak position q* for PEP–PDMS diblocks in the BBC phase. The sample was annealed for many months at room temperature before the trace marked “heating”. The sample was then cooled back (black squares) and departed from equilibrium below 150 °C. The sample in diamonds was quenched from 180 to 40 °C before heat. (b) Long-term annealing for q* for the sample in panel a, after cooling to 40 °C. Reproduced with permission from ref (65). Copyright 2003 Wiley.

Figure 7

Time–temperature transformation diagram for a PEP–PDMS diblock subject to long-time annealing after various temperature quenches. The equilibrium phases are BCC and σ, but the latter takes increasingly long times to emerge at lower temperatures. This is attributed in part to slow dynamics; the red dashed line indicates the estimated chain exchange time. Reproduced with permission from ref (74). Copyright 2021 American Chemical Society.

Figure 8

Residence time of individual surfactants in micelles for a variety of systems, as a function of carbon number m. Figure reconstructed from Figure 3.8 in ref (30).

Figure 9

(a) Schematic illustration of the time-resolved SANS experiment, where red denotes a deuterated core block, blue a normal core block, and purple a solvent containing sufficient deuterium to contrast-match a 50:50 deuterated:normal core. (b) SANS traces as a function of time, after blending two micelle populations (in this case, PMMA-b-PnBMA in [C₂mim][TFSI]). Note that the infinite time data correspond to a sample in which the deuterated and normal BCPs were blended in advance. The fact that this SANS trace does not match the solvent is due to residual scattering from the PMMA coronas. (c) Relaxation functions R(t) for equivalent blended samples at different temperatures. (d) Master curve obtained by horizontal shifting of the data in panel c with T_ref = 35 °C. The dashed curve is a fit to the model described by eq 4. Data reproduced with permission from ref (95). Copyright 2016 American Chemical Society.

Figure 10

TR-SANS relaxation function for two PS-PEP samples, with fits to eq 4. The extracted value of χ is independent of N if the barrier is taken as increasing linearly with N_core. Figure reconstructed from data in ref (98).

Figure 11

Effect of N_corona on chain exchange: (a) C₂₄–PEO in water and (b) PS-PEP in squalene. The two systems show opposite trends. Figures reproduced with permission from ref (100), copyright 2016 American Chemical Society, and ref (101), copyright 2018 American Chemical Society, respectively.

Figure 12

(a) Dependence of barrier divided by N_core, αf(χ), on the independently determined χ, for PnBMA-PMMA in [C₂mim][TFSI]. (b) Enthalpy penalty of chain expulsion for SEP micelles in binary mixed solvents, comparing the fitted results from TR-SANS (f(χ)⟨N_core⟩) and calculated values by the Flory–Huggins theory (a(χ – v2/v1) ⟨N_core⟩. Figures reproduced with permission from ref (95), copyright 2016 American Chemical Society, and ref (102), copyright 2020 American Chemical Society, respectively.

Figure 13

(a) Free energy of a single A₄B₈ BCP as a function of the distance between the block junction and the micelle center-of-mass, as a function of the core–solvent energy. Data reported in ref (114), corrected for the entropy of the spherical shell. (b) Stretching of the core block as a function of position. Figure reproduced with permission from ref (114). Copyright 2021 American Chemical Society.

Figure 14

Schematic “reaction coordinate” for fusion/fragmentation, for micelles of sizes Q₁ and Q₂; fusion is favored in this case, as ΔF > 0, following Dormidontova. The barrier increases as Q₁Q₂^1/2; the time for one corona to penetrate the other to a distance L provides τ_frag,0.

Figure 15

(a) Relaxation rates k_decay versus the concentration of P103 empty micelles for various temperatures: 21, 23, 26, and 30 °C. The concentration of micelles is given by ([micelles] = ([P103] – cmc)/N_agg. (b) Rate of fragmentation k_frag (□) and the rate of fusion k_fus (■) vs the inverse of the absolute temperature for P103. Figures reproduced with permission from ref (144). Copyright 2021 American Chemical Society.

Figure 16

Liquid cell TEM images of a phenyl-b-peptide-co-hydroxyl amphiphilic BCP undergoing fusion in aqueous media. Reproduced with permission from ref (148). Copyright 2017 American Chemical Society.

Figure 17

(a) Synchrotron SAXS for 0.25 wt % BO(25–22) in [C₂mim][TFSI] at 170 °C; (b) normalized ⟨R_core⟩ from SAXS upon T-jump to 170 °C for 0.5 wt % BO(8–7) in 1-alkyl-3-methylimidazolium [TFSI]-based ionic liquids. The curves are shifted vertically for clarity. Solid lines represent the fits to the relaxation function shown in eq 5 with an Avrami exponent of n = 2. Figures reproduced with permission from refs (151), copyright 2020 American Chemical Society, and (152), copyright 2019 American Chemical Society, respectively.

Figure 18

Fragmentation times for symmetric BO diblocks in [C₂mim][TFSI] as a function of total molecular weight, with the best fit power law. Reproduced with permission from ref (153). Copyright 2021 American Chemical Society.

Figure 19

Time evolution of micelle cores for BO(25–22) in [C₂mim][TFSI] annealed at 170 °C directly in the TEM instrument. Suggested pathway for fragmentation is shown below the images. Reproduced with permission from ref (151). Copyright 2020 American Chemical Society.