Dissecting the general mechanisms of protein cage self-assembly by coarse-grained simulations

Abstract

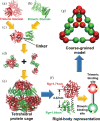
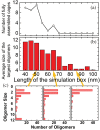
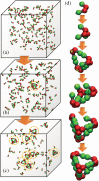
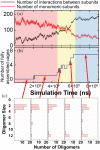
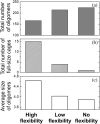
The development of artificial protein cages has recently gained massive attention due to their promising application prospect as novel delivery vehicles for therapeutics. These nanoparticles are formed through a process called self-assembly, in which individual subunits spontaneously arrange into highly ordered patterns via non-covalent but specific interactions. Therefore, the first step toward the design of novel engineered protein cages is to understand the general mechanisms of their self-assembling dynamics. Here we have developed a new computational method to tackle this problem. Our method is based on a coarse-grained model and a diffusion-reaction simulation algorithm. Using a tetrahedral cage as test model, we showed that self-assembly of protein cage requires of a seeding process in which specific configurations of kinetic intermediate states are identified. We further found that there is a critical concentration to trigger self-assembly of protein cages. This critical concentration allows that cages can only be successfully assembled under a persistently high concentration. Additionally, phase diagram of self-assembly has been constructed by systematically testing the model across a wide range of binding parameters. Finally, our simulations demonstrated the importance of protein's structural flexibility in regulating the dynamics of cage assembly. In summary, this study throws lights on the general principles underlying self-assembly of large cage-like protein complexes and thus provides insights to design new nanomaterials.

Keywords: coarse-grained simulation; complex assembly; conformational flexibility; protein cage.

FIGURE 1

An artificially designed protein cage is used to test our simulations. Each subunit of the cage consists of two structural domains. One from bromoperoxidase enzyme can form homo‐trimers with three‐fold symmetry (a). The other from viral matrix protein can be dimerized (b). Two domains are fused together by a semi‐flexible linker (c). Through the combination of trimeric and dimeric interactions (d), all 12 subunits can be spatially arranged into tetrahedral shape (e). The PDB id of the entire cage complex is 4ITV. Self‐assembly of the cage is studied by a coarse‐grained model, in which the structure of each subunit is simplified by two spherical rigid bodies (f). The conformation of a fully assembly cage based on this rigid‐body representation is illustrated in (g)

FIGURE 2

We evaluated the functions of binding affinities in regulating cage assembly. We fixed association rates and tuned dissociation rates into different values. Seven specific values were adopted for both dimeric and trimeric interactions. Our simulation results of all combinations are summarized as the two‐dimensional color contours. Dissociation rates of trimeric and dimeric interactions are indexed along the X‐axis and the Y‐axis of each contour, respectively. Given a specific combination of dissociation rates, the detailed value of an indicator is coded by the color bar listed on the right side of each corresponding panel. The average numbers of monomeric subunits left at the end of all trajectories are plotted in (a); the average numbers of oligomers formed at the end of all trajectories are plotted in (b); the average size of oligomers formed at the end of all trajectories are plotted in (c); and the total numbers of full‐size cages obtained from all trajectories are plotted in (d)

FIGURE 3

We further fixed the total number of subunits in the system and changed the size of the simulation box to illustrate the effect of concentration on assembly. The correlation between the concentration and total number of obtained full‐size cages is plotted in (a), while the correlation between the concentration and the average size of the largest oligomers in each corresponding system is plotted in (b). The figures show that a small decrease of box size from 60 to 50 nm led to a dramatic increase in the number of full‐size cages, suggesting that there is a phase transition taking place in the process of cage assembly from a state only consisting of small oligomers to a state that full‐size cages can be effectively assembled. The histograms of oligomer size at different box sizes are further plotted in (c) as a function of the oligomer number that belongs to the corresponding size

FIGURE 4

Based on the coarse‐grained model, the simulation of cage assembly was started from an initial random configuration (a). A representative snapshot in the middle of the assembling pathway was plotted in (b), and the final configuration at the end of the simulation trajectory is shown in (c). Fully assembled cages are highlighted by orange dashed circles in these plots. We also traced the kinetic pathways of how these cages were formed. One typical pathway is illustrated in (d)

FIGURE 5

The kinetics profiles of cage assembly are displayed as a function of simulation time. In (a), the total number of interactions formed between subunits along the trajectory is shown as black curve, while the red curve indicates the total number of monomeric subunits left in the system. The total number of successfully formed full‐size cages is plotted in (b) at different simulation time. Based on the kinetic profiles, three stages of self‐assembling process were identified, corresponding to the three colored panels in the figure. The oligomer size distribution is further traced along the simulation. The histograms of oligomer size at some selective time points are plotted in (c) as a function of the oligomer number that belongs to the corresponding size

FIGURE 6

We have performed a computational experiment in which the flexibility of the linker between two domains in a subunit was tuned in three separate simulation scenarios. In the first scenario, the flexibility was set to a high level. In the second scenario, the flexibility was set to a low level, while in the last scenario, the flexibility was turned off. Multiple (20) trajectories were carried out under each scenario, and simulation results are compared as histograms among different scenarios. Specifically, we compared the total numbers of oligomers formed at the end of all simulations (a), the total number of fully assembled cages observed at the end of all simulations (b), and the average size of all oligomers formed at the end of simulations (c). The scenario of high flexibility is shown by the left columns. The scenario of low flexibility is shown by the middle columns. The scenario of low flexibility is shown by the right columns