Hyperchaos, Intermittency, Noise and Disorder in Modified Semiconductor Superlattices

Abstract

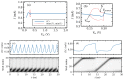
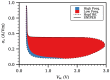
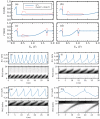
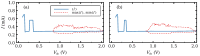
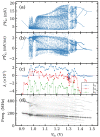
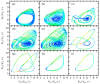
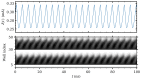
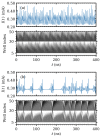
Weakly coupled semiconductor superlattices under DC voltage bias are nonlinear systems with many degrees of freedom whose nonlinearity is due to sequential tunneling of electrons. They may exhibit spontaneous chaos at room temperature and act as fast physical random number generator devices. Here we present a general sequential transport model with different voltage drops at quantum wells and barriers that includes noise and fluctuations due to the superlattice epitaxial growth. Excitability and oscillations of the current in superlattices with identical periods are due to nucleation and motion of charge dipole waves that form at the emitter contact when the current drops below a critical value. Insertion of wider wells increases superlattice excitability by allowing wave nucleation at the modified wells and more complex dynamics. Then hyperchaos and different types of intermittent chaos are possible on extended DC voltage ranges. Intrinsic shot and thermal noises and external noises produce minor effects on chaotic attractors. However, random disorder due to growth fluctuations may suppress any regular or chaotic current oscillations. Numerical simulations show that more than 70% of samples remain chaotic when the standard deviation of their fluctuations due to epitaxial growth is below 0.024 nm (10% of a single monolayer) whereas for 0.015 nm disorder suppresses chaos.

Keywords: chaos; chaos design; chaotic devices; fast true random number generators; fluctuations; hyperchaos; intermittency; nonlinear electron transport; secure communications; semiconductor superlattices.

Figure 1

(a) First plateau of the current–voltage characteristics for the SSL with 50 identical periods. (b) Zoom of the region of self-oscillations that appear as a supercritical Hopf bifurcation and end at a SNIPER. $V_d$ is the voltage at which the frequency of the oscillations drop to lower values. For $V_{dc}>V_d$, the high electric field domains move throughout the SSL and reach the collector contact. Current traces and the corresponding density plots of the electric field for (c) $V_{dc}=0.26\mathrm{V}$ (just after the Hopf bifurcation) and (d) $V_{dc}=0.29\mathrm{V}$ (just before the SNIPER bifurcation). Light and dark tones correspond to low and high field values, respectively.

Figure 2

Phase diagram of injector contact conductivity versus DC voltage exhibiting a bounded region of current self-oscillations. At the dashed boundary line, the self-oscillations appear as Hopf bifurcations from the stationary field profile which is linearly stable outside the bounded region. The continuous boundary line corresponds to oscillations disappearing at a saddle-node infinite period bifurcation, as selected in the main text. In the red regions, self-oscillations have low frequency and correspond to fully formed charge dipole waves that move across the entire SSL. In the blue regions, high frequency self-oscillations correspond to charge dipole waves that disappear before reaching the receiving contact. Reprinted from [21].

Figure 3

Tunneling current–voltage characteristics for the ideal SSL with $n_i=N_D$, $V_i=V$ comparing the reference configuration (ref.) $d_B=4$ nm, $d_W=7$ nm to the contact Ohm’s law (dot-dashed straight line) and to other configurations with more or less monolayers (m.l.) at the wells. The rhombus marks the critical current $J_{\mathrm{cr}}$ and voltage $V_{\mathrm{cr}}$ at which the contact Ohm’s law intersects the reference configuration. Reprinted from [21].

Figure 4

First plateau of the current–voltage characteristics for the SSL with 50 identical periods when the modified 10 nm-wide well is at: (a) $i_w=5$, (b) $i_w=20$, (c) $i_w=30$, and (d) $i_w=39$. Current traces and density plots of the electric field for: (e) $i_w=20$, $V_{dc}=0.23\mathrm{V}$; (f) $i_w=20$, $V_{dc}=0.5\mathrm{V}$; (g) $i_w=30$, $V_{dc}=0.5\mathrm{V}$; (h) $i_w=39$, $V_{dc}=1.02\mathrm{V}$. In the density plots, light and dark tones correspond to low and high field values, respectively.

Figure 5

First plateau of the current–voltage characteristics for the SSL with 50 identical periods with modified 10 nm-wide wells at $i_1=5$ and: (a) $i_2=25$, (b) $i_2=30$. The presence of two modified wells gives rise to two peaks in the low voltage, stationary, part of the $I-V$ characteristic curve. In case (a), self-oscillations are time periodic. In case (b), self-oscillations are time periodic for $V_{dc}<1$ V and for $V_{dc}>1.5$ V, and they are complex (mostly chaotic) for $1<V_{dc}<1.5$ V.

Figure 6

(a) Poincaré map from $V_{42}\left(t\right)$, (b) Poincaré map from ${\dot{V}}_{42}\left(t\right)$, (c) Lyapunov exponents, and (d) Fourier spectrum as functions of DC voltage for the modified SSL with $i_1=5$ and $i_2=30$. Each panel shows features hidden in the other ones. The Poincaré map reveals jumps between periodic attractors at $V_{dc}=1.3\mathrm{V}$ and $V_{dc}=1.43\mathrm{V}$. The Fourier spectrum reveals the underlying behavior to be quasi-periodic with different incommensurate frequencies, whereas the Lyapunov exponents show that the system is hyperchaotic for $V_{dc}<1.08\mathrm{V}$ (${\lambda }_1,{\lambda }_2>0$ and of comparable scales). For $V_{dc}>1.08\mathrm{V}$, the system has intermittent chaos at different time-scales (${\lambda }_1\gg {\lambda }_2\approx 0$). Reprinted from [21].

Figure 7

Phase plane portraits $(V_{15},V_{35})$ for $V_{dc}=$ (a) 1.01 V, (b) 1.03 V, (c) 1.10 V, (d) 1.20 V, (e) 1.275 V, (f) 1.30 V, (g) 1.40 V, (h) 1.45 V, (i) 1.50 V.

Figure 8

Current traces and density plots of the electric field profile for $V_{dc}=0.9$ V. For this low voltage periodic attractor, the waves at regions II and III do not reach $i_2$ or the collector, respectively. In the density plots, light and dark tones correspond to low and high field values, respectively. Reprinted from [21].

Figure 9

Current traces and density plots of the electric field for (a) $V_{dc}=1.01$ V (hyperchaos, two positive Lyapunov exponents) and (b) $V_{dc}=1.20$ V (intermittency, one positive and one zero Lyapunov exponent). In the density plots, light and dark tones correspond to low and high field values, respectively. Reprinted from [21].

Figure 10

Success rate measuring fraction of simulations where chaotic attractor remains for a given value of the standard deviation $\sigma$. Reprinted from [21].

Figure 11

Effect of shot and thermal noise on the three largest Lyapunov exponents (noiseless values marked by tilted triangles) for (a) $V_{dc}=0.98\mathrm{V}$ (hyperchaos) and (b) $V_{dc}=1.15\mathrm{V}$ (intermittent chaos). The boxes describe the distribution of exponents and the vertical bars indicate the standard deviation of fluctuations.