VeVaPy, a Python Platform for Efficient Verification and Validation of Systems Biology Models with Demonstrations Using Hypothalamic-Pituitary-Adrenal Axis Models
- PMID: 36554152
- PMCID: PMC9777964
- DOI: 10.3390/e24121747
VeVaPy, a Python Platform for Efficient Verification and Validation of Systems Biology Models with Demonstrations Using Hypothalamic-Pituitary-Adrenal Axis Models
Abstract
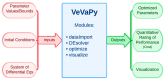
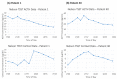
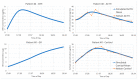
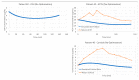
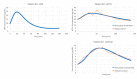
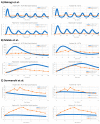
In order for mathematical models to make credible contributions, it is essential for them to be verified and validated. Currently, verification and validation (V&V) of these models does not meet the expectations of the system biology and systems pharmacology communities. Partially as a result of this shortfall, systemic V&V of existing models currently requires a lot of time and effort. In order to facilitate systemic V&V of chosen hypothalamic-pituitary-adrenal (HPA) axis models, we have developed a computational framework named VeVaPy-taking care to follow the recommended best practices regarding the development of mathematical models. VeVaPy includes four functional modules coded in Python, and the source code is publicly available. We demonstrate that VeVaPy can help us efficiently verify and validate the five HPA axis models we have chosen. Supplied with new and independent data, VeVaPy outputs objective V&V benchmarks for each model. We believe that VeVaPy will help future researchers with basic modeling and programming experience to efficiently verify and validate mathematical models from the fields of systems biology and systems pharmacology.
Keywords: HPA axis; Major Depressive Disorder; Python; Verification & Validation; differential equations model; stress test.
Conflict of interest statement
The authors declare no conflict of interest.
Figures





References
-
- Thacker B.H., Doebling S.W., Hemez F.M., Anderson M.C., Pepin J.E., Rodriguez E.A. In: Concepts of Model Verification and Validation. Schaller C., editor. US Department of Energy, Los Alamos National Laboratory; Los Alamos, NM, USA: 2004. Report No.: LA-14167-MS;
-
- IWGFR . Specialists’ Meeting on Predictions and Experience of Core Distortion Behaviour 1–4 October 1984. International Atomic Energy Agency; Wilmslow, UK: 1984.
-
- Nakagawa M. Verification and Validation of Core Mechanical Performance Code ARKAS with IAEA Benchmark Problems, (II) J. Nucl. Sci. Technol. 1993;30:389–412. doi: 10.1080/18811248.1993.9734497. - DOI
-
- Hohne T., Kliem S., Bieder U. IAEA CRP benchmark of ROCOM PTS test case for the use of CFD in reactor design using the CFD-Codes ANSYS CFX and TrioCFD. Nucl. Eng. Des. 2018;333:161–180. doi: 10.1016/j.nucengdes.2018.04.017. - DOI
-
- Schwer L.E. An overview of the PTC 60/V&V 10: Guide for verification and validation in computational solid mechanics. Eng. Comput. 2007;23:245–252. doi: 10.1007/s00366-007-0072-z. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

