Robustness of Interdependent Networks with Weak Dependency Based on Bond Percolation

Abstract

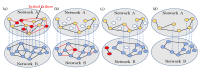
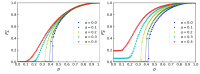
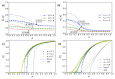
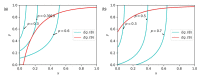
Real-world systems interact with one another via dependency connectivities. Dependency connectivities make systems less robust because failures may spread iteratively among systems via dependency links. Most previous studies have assumed that two nodes connected by a dependency link are strongly dependent on each other; that is, if one node fails, its dependent partner would also immediately fail. However, in many real scenarios, nodes from different networks may be weakly dependent, and links may fail instead of nodes. How interdependent networks with weak dependency react to link failures remains unknown. In this paper, we build a model of fully interdependent networks with weak dependency and define a parameter α in order to describe the node-coupling strength. If a node fails, its dependent partner has a probability of failing of 1−α. Then, we develop an analytical tool for analyzing the robustness of interdependent networks with weak dependency under link failures, with which we can accurately predict the system robustness when 1−p fractions of links are randomly removed. We find that as the node coupling strength increases, interdependent networks show a discontinuous phase transition when α<αc and a continuous phase transition when α>αc. Compared to site percolation with nodes being attacked, the crossover points αc are larger in the bond percolation with links being attacked. This finding can give us some suggestions for designing and protecting systems in which link failures can happen.

Keywords: bond percolation; complex networks; giant connected component; robustness; weak dependency.

Figure 1

Schematic illustration of cascading failure in interdependent networks. Network A and Network B are fully dependent, as shown by the dependency links, which are represented as blue lines in the figure. The nodes in both networks are initially functional. (a) Initial failures occur in Network A. The red edges are failed edges. The red nodes failed because all of their links were removed. (b) The failed nodes were removed, while the nodes’ links that depended on the failed nodes of another network had a probability of failing of $1-\alpha$. (c) Nodes that were not located in the giant components lost function. (d) The network eventually reached a stable state, and the remaining nodes were all located in the giant connected components.

Figure 2

The sizes of the giant components $P_A^{\infty }$ (left) and $P_B^{\infty }$ (right) in coupled ER networks with $\langle k_A\rangle =\langle k_B\rangle =4$ when a fraction of $1-p$ of the links were randomly removed from network A. The solid lines represent the theoretical predictions. The symbols represent simulation results from 40 iterations on networks with ${10}^5$ nodes.

Figure 3

The sizes of the giant components $P_A^{\infty }$ (left) and $P_B^{\infty }$ (right) in coupled SF networks with $k_{min}=2,k_{max}=2000$ and $\lambda =2.7$ when a fraction of $1-p$ of the links were randomly removed from network A. The solid lines represent the theoretical predictions. The symbols represent the simulation results from 40 iterations on networks with ${10}^5$ nodes.

Figure 4

A comparison of bond percolation and site percolation. (a) Percolation thresholds of ER networks. The dashed lines represent site percolation, while the solid lines represent bond percolation. Different colors of lines represent different average degrees $\langle k\rangle$ of the ER networks. (b) Percolation thresholds of SF networks, the power law of which is $\lambda =2.7$ and the maximum values of degrees of which are $k_{max}=316$. Different colors of the different lines represent different minimum degrees of the SF networks. The crossover points for bond percolation are marked on the corresponding curves. (c) Sizes of giant connected components after a fraction of $1-p$ sites or bonds are removed in ER networks. The solid lines represent bond percolation and the dashed lines represent site percolation. (d) Sizes of giant connected components after a fraction of $1-p$ sites or bonds are removed in SF networks.

Figure 5

Bond percolation in interdependent networks with weak dependency. The red line represents Equation (11), and it is not affected by p when $\alpha$ is a constant value. The blue lines represent Equation (10). (a) As p increases from 0 to 1 when $\alpha <{\alpha }_c$, the two curves have a tangent point. (b) However, when $\alpha >{\alpha }_c$, the solutions of the two equations continuously decrease to 0.