Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety

Abstract

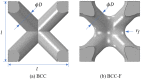
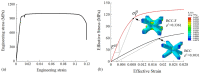
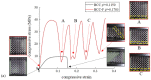
This paper presents a new framework for lightweight optimisation of functionally graded lattice structures (FGLSs) with a particular focus on enhancing and guaranteeing structural safety through three main contributions. Firstly, a design strategy of adding fillets to the joints of body-centred cubic (BCC) type lattice cells was proposed to improve the effective yield stress of the lattices. Secondly, effective properties of lattice metamaterials were experimentally characterised by conducting quasi-static uniaxial compression tests on selective laser melted specimens of both Ti6Al4V BCC and filleted BCC (BCC-F) lattices with different relative densities. Thirdly, a yield stress constraint for optimising FGLSs was developed based on surrogate models quantifying the relationships between the relative density and the effective properties of BCC and BCC-F lattices developed using experimental results assisted by numerical homogenisation. This framework was tested with two case studies. Results showed that structural safety with respect to avoiding yield failure of the optimised FGLSs can be ensured and the introduction of fillets can effectively improve the strength-to-weight ratio of the optimised FGLSs composed of BCC type lattices. The BCC-F FGLS achieved 14.5% improvement in weight reduction compared with BCC FGLS for the Messerschmitt-Bölkow-Blohm beam optimisation case study.

Keywords: additive manufacturing; filleted lattice metamaterials; functionally graded lattice structure; structural optimisation; yield stress constraint.

Figure 1

Flowchart of the yield constrained FGLS optimisation framework with experimentally characterised BCC and BCC-F lattice metamaterials. $D^{\prime }$ and $N_f$ denote relative strut diameter and fillet parameter, respectively, which are defined in the next subsection (through Equations (1) and (2), respectively). FE, AM, RVE, PBC, FGLS denote finite element, additive manufacturing, representative volume element, periodic boundary condition, and functionally graded lattice structure, respectively.

Figure 2

Configurations of (a) a BCC lattice cell and (b) a BCC-F lattice cell, shown in the front view, where $l$, $D$, and $r_f$ denote the length of the lattice cell, the lattice strut diameter, and the fillet radius, respectively.

Figure 3

The stress–strain curves of (a) parent material, i.e., SLM fabricated Ti6Al4V, for lattice metamaterials, and (b) examples of a BCC-F and a BCC lattice RVEs, where $E^H$ and ${\sigma }_Y^H$ are the effective Young’s modulus and the effective yield stress, respectively. The stress–strain curves of the parent material and the example RVEs were obtained experimentally and numerically, respectively.

Figure 4

Effect of the fillet parameter, $N_f$, on the normalised effective yield stress, ${\overline{\sigma }}_Y$, of the BCC type lattice at different relative density (${\rho }^{\prime }$ ) levels. At each ${\rho }^{\prime }$ level, the yield stress values are normalised by the yield stress of the BCC lattice without fillets.

Figure 5

Demonstration of (a) dimensions of lattice specimen design and (b) CAD models (front view) of BCC and BCC-F specimen designs, where $D_{ds}^{\prime }$ and ${\rho }_{ds}^{\prime }$ represent designed values of relative strut diameter and relative density, respectively.

Figure 6

Cracks observed on a high relative density (${\rho }_{ds}^{\prime }=0.7$) BCC lattice specimen after fabrication.

Figure 7

Demonstration of SLM fabricated BCC and BCC-F lattice specimens with different measured relative densities (${\rho }_{ms}^{\prime }$).

Figure 8

Experimental setup of the quasi-static uniaxial compression tests on the specimens constructed by BCC and BCC-F lattices at room temperature.

Figure 9

Experimental results of the compressive stress–strain (engineering) curves of specimens of (a) BCC lattice with ${\rho }^{\prime }$ = 0.1150, BCC-F lattice with ${\rho }^{\prime }$ = 0.1783, (b) BCC lattice with ${\rho }^{\prime }$ = 0.3272, BCC-F lattice with ${\rho }^{\prime }$ = 0.3700, and (c) BCC lattice with ${\rho }^{\prime }$ = 0.5328, BCC-F lattice with ${\rho }^{\prime }$ = 0.5590, associated with demonstrations of deformation processes and fracture modes.

Figure 9

Experimental results of the compressive stress–strain (engineering) curves of specimens of (a) BCC lattice with ${\rho }^{\prime }$ = 0.1150, BCC-F lattice with ${\rho }^{\prime }$ = 0.1783, (b) BCC lattice with ${\rho }^{\prime }$ = 0.3272, BCC-F lattice with ${\rho }^{\prime }$ = 0.3700, and (c) BCC lattice with ${\rho }^{\prime }$ = 0.5328, BCC-F lattice with ${\rho }^{\prime }$ = 0.5590, associated with demonstrations of deformation processes and fracture modes.

Figure 10

Experimental (symbols) and numerical homogenisation (solid lines) results of (a) the relative effective Young’s moduli (log-log scale), (b) the relative effective yield stresses (log–log scale), and (c) the effective Poisson’s ratios (linear scale) of the BCC and the BCC-F lattices at different relative density levels.

Figure 11

The corrected relative effective shear moduli and the corresponding numerically homogenised relative effective shear moduli of the BCC lattice and the BCC-F lattices at different relative densities (log–log scale).

Figure 12

Relationship between the relative density, ${\rho }^{\prime }$, and the effective material properties of (a) $C_{11}^E$, (b) $C_{12}^E$, (c) $C_{44}^E$, and (d) 0.2% offset yield stress, ${\sigma }_Y^E$, of the BCC and the BCC-F lattices. Symbols represent the properties measured and calculated at specific density levels and dashed lines represent the plots of second-order polynomial surrogate models fitting the symbols.

Figure 13

Flowchart of the optimisation platform.

Figure 14

Dimensions and boundary conditions sketch of the L-shaped beam bending case study [49].

Figure 15

Optimisation results of the BCC-F L-shaped beam bending case study with problem ${\mathbb{P}}_A\left(v_f=0.25\right)$: distributions of (a) optimised relative density ($\overline{C}$ is normalised optimised compliance) and (b) von Mises stress, and (c) the volume proportion histogram of stress constraint measurement (${\sigma }_{VM}/{\widehat{\sigma }}_Y$ ) with the yield stress constraint applied; distributions of (d) optimised relative density and (e) von Mises stress, and (f) the volume proportion histogram of ${\sigma }_{VM}/{\widehat{\sigma }}_Y$ without yield stress constraint.

Figure 16

Detailed CAD model of the optimised BCC-F L-shaped beam with (a) front view and (b) perspective view.

Figure 17

Dimensions and boundary conditions sketch of the MBB beam (half model with the symmetric boundary condition applied) bending case study.

Figure 18

Comparisons of (a,d) the relative density (${\tilde{\rho }}^{\prime }$) distributions and the optimised volume fractions ($V_{opt}$ ), (b,e) the von Mises stress (${\sigma }_{VM}$ ) contours, and (c,f) the volume proportion histogram of ${\sigma }_{VM}/{\widehat{\sigma }}_Y$ for the optimised MBB beam with the BCC (the top row) and the BCC-F (the bottom row) lattices.