Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Dec 11;14(24):5426.
doi: 10.3390/polym14245426.

Holographic Lens Resolution Using the Convolution Theorem

Tomás Lloret  1 , Marta Morales-Vidal  2 , Víctor Navarro-Fuster  3 , Manuel G Ramírez  2   3 , Augusto Beléndez  2   3 , Inmaculada Pascual  1   2
Affiliations

Holographic Lens Resolution Using the Convolution Theorem

Tomás Lloret et al. Polymers (Basel). .

Abstract

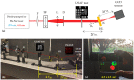
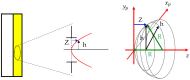
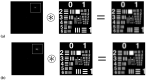
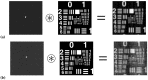
The similarity between object and image of negative asymmetrical holographic lenses (HLs) stored in a low-toxicity photopolymer has been evaluated theoretically and experimentally. Asymmetrical experimental setups with negative focal lengths have been used to obtain HLs. For this purpose, the resolution of the HLs was calculated using the convolution theorem. A USAF 1951 test was used as an object and the impulse responses of the HLs, which in this case was the amplitude spread function (ASF), were obtained with two different methods: using a CCD sensor and a Hartmann Shack (HS) wavefront sensor. For a negative asymmetrically recorded HL a maximum resolution of 11.31 lp/mm was obtained. It was evaluated at 473 nm wavelength. A theoretical study of object-image similarity had carried out using the MSE (mean squared error) metric to evaluate the experimental results obtained quantitatively.

Keywords: convolution theorem; holographic lenses; resolution; volume holography.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Biophotopol chemical structures of the prepolymer components. PVA: polyvinyl alcohol, NaAO: sodium acrylate, TEA: triethanolamine, RF: riboflavin 5’- monophosphate sodium salt.
Figure 2
Figure 2
(a) Experimental setup for the HLs resolution evaluation. F: filter, SF: spatial filter, L: lens, D: diaphragm, HL: holographic lens, CCD Sensor: Charge Coupled Device. (b) Real photo of the experimental setup. (c) Picture of HL stored on the photopolymer layer. Video of HL stored on the photopolymer layer can be seen in S1.
Figure 3
Figure 3
Geometry for obtaining the impulse response (ASF) of the HLs.
Figure 4
Figure 4
Geometry for the relation between the ideal sagittal, the real sagittal and the wave aberration function (W). The wave aberration (W) is also related to the ray aberration (Δ(x,y)).
Figure 5
Figure 5
Simulated convolution for negative asymmetrical HLs, with ASF obtained with the HS wavefront sensor, reconstructed at (a) 473 nm and (b) 633 nm.
Figure 6
Figure 6
Simulated convolution for negative asymmetrical HLs, with ASF obtained with the CCD sensor, reconstructed at: (a) 473 nm, (b) 633 nm.
Figure 7
Figure 7
Image obtained with the CCD sensor illuminated at: (a) 473 nm, (b) 633 nm.
Figure 8
Figure 8
Convolution simulations of an object test (University of Alicante logo) with the ASFs obtained by the different methods (HS wavefront sensor and CCD sensor) using as reconstruction wavelength: (a) 473 nm and (b) 633 nm.
Figure 9
Figure 9
Convolution simulations of an object test (University of Alicante logo) with the ASFs obtained by the different methods: HS wavefront sensor and CCD sensor.
See this image and copyright information in PMC

References

    1. Gabor D. A New Microscopic Principle. Nature. 1948;161:777–779. doi: 10.1038/161777a0. - DOI - PubMed
    1. Barachevsky V.A. The Current Status of the Development of Light-Sensitive Media for Holography (a Review) Opt. Spectroc. 2018;124:373–407. doi: 10.1134/S0030400X18030062. - DOI
    1. Schwar M.J.R., Pandya T.P., Weinberg F.J. Point holograms as optical elements. Nature. 1967;215:239–241. doi: 10.1038/215239a0. - DOI
    1. Store T.W., Thompson B.J. Holographic and diffractive lenses and mirrors. SPIE Milestore Ser. 1991;34:3–668.
    1. Denisyuk Y.N. Photographic Reconstruction of the Optical Properties of an Object in Its Own Scattered Radiation Field. Sov. Phys. Dokl. 1962;7:543–545.

LinkOut - more resources