Vehicle Stability Analysis under Extreme Operating Conditions Based on LQR Control

Abstract

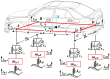
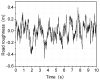
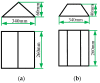
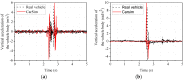
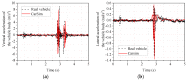
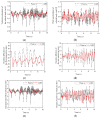
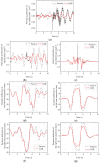
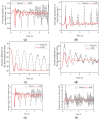
Under extreme working conditions such as high-speed driving on roads with a large road surface unevenness coefficient, turning on a road with a low road surface adhesion coefficient, and emergency acceleration and braking, a vehicle's stability deteriorates sharply and reduces ride comfort. There is extensive existing research on vehicle active suspension control, trajectory tracking, and control methods. However, most of these studies focus on conventional operating conditions, while vehicle stability analysis under extreme operating conditions is much less studied. In order to improve the stability of the whole vehicle under extreme operating conditions, this paper investigates the stability of a vehicle under extreme operating conditions based on linear quadratic regulator (LQR) control. First, a seven degrees of freedom (7-DOF) dynamics model of the whole vehicle is established based on the use of electromagnetic active suspension, and then an LQR controller of the electromagnetic active suspension is designed. A joint simulation platform incorporating MATLAB and CarSim was built, and the CarSim model is verified by real vehicle tests. Finally, the stability of the vehicle under four different ultimate operating conditions was analyzed. The simulation results show that the root mean square (RMS) values of body droop acceleration and pitch angle acceleration are improved by 57.48% and 28.81%, respectively, under high-speed driving conditions on Class C roads. Under the double-shift condition with a low adhesion coefficient, the RMS values of body droop acceleration, pitch acceleration, and roll angle acceleration are improved by 58.25%, 55.41%, and 31.39%, respectively. These results indicate that electromagnetic active suspension can significantly improve vehicle stability and reduce driving risk under extreme working conditions when combined with an LQR controller.

Keywords: CarSim; LQR controller; extreme operating conditions; vehicle stability.

Figure 4

Schematic diagram of the location of the double shift line test pile.

Figure 1

Schematic of the 7-DOF full-car suspension system.

Figure 2

Schematic of the electromagnetic active suspension with LQR controller.

Figure 3

Block diagram of CarSim and Simulink joint simulation.

Figure 5

Obtained random road excitation for a Class C road.

Figure 6

Road test of the vehicle. (a) vehicle test ground; (b) experimental vehicle; (c) computer; (d) dynamic signal collector.

Figure 6

Road test of the vehicle. (a) vehicle test ground; (b) experimental vehicle; (c) computer; (d) dynamic signal collector.

Figure 7

Diagram of speed reduction belt. (a) triangular speed reduction belt; (b) trapezoidal speed reduction belt.

Figure 8

Response of the body when passing over a triangular speed bump. (a) vertical acceleration of the body; (b) lateral camber acceleration of the body.

Figure 9

Trapezoidal speed bump body response. (a) vertical acceleration of the body; (b) lateral camber acceleration of the body.

Figure 10

Simulated time domain response of high-speed conditions on Class C roads. (a) body vertical acceleration; (b) body pitch angle acceleration; (c) front suspension dynamic deflection; (d) rear suspension dynamic deflection; (e) front wheel tire dynamic load; (f) rear wheel tire dynamic load.

Figure 11

Simulated time domain response of low adhesion coefficient double shift line condition. (a) body vertical acceleration; (b) body pitch acceleration; (c) body lateral camber acceleration; (d) left front suspension dynamic deflection; (e) left rear suspension dynamic deflection; (f) right front suspension dynamic deflection; (g) right rear suspension dynamic deflection; (h) left front tire dynamic load; (i) left rear tire dynamic load; (j) right front tire dynamic load; (k) right rear tire dynamic load.

Figure 11

Simulated time domain response of low adhesion coefficient double shift line condition. (a) body vertical acceleration; (b) body pitch acceleration; (c) body lateral camber acceleration; (d) left front suspension dynamic deflection; (e) left rear suspension dynamic deflection; (f) right front suspension dynamic deflection; (g) right rear suspension dynamic deflection; (h) left front tire dynamic load; (i) left rear tire dynamic load; (j) right front tire dynamic load; (k) right rear tire dynamic load.

Figure 12

Simulated time domain response of emergency acceleration condition. (a) body vertical acceleration; (b) body pitch angle acceleration; (c) front suspension dynamic deflection; (d) rear suspension dynamic deflection; (e) front wheel tire dynamic load; (f) rear wheel tire dynamic load.

Figure 13

Simulated time domain response of emergency braking condition. (a) body vertical acceleration; (b) body pitch angle acceleration; (c) front suspension dynamic deflection; (d) rear suspension dynamic deflection; (e) front wheel tire dynamic load; (f) rear wheel tire dynamic load.

Figure 13

Simulated time domain response of emergency braking condition. (a) body vertical acceleration; (b) body pitch angle acceleration; (c) front suspension dynamic deflection; (d) rear suspension dynamic deflection; (e) front wheel tire dynamic load; (f) rear wheel tire dynamic load.