Plasmonic Sensors beyond the Phase Matching Condition: A Simplified Approach

Abstract

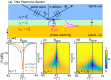
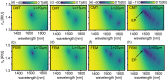
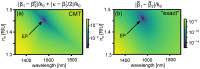
The conventional approach to optimising plasmonic sensors is typically based entirely on ensuring phase matching between the excitation wave and the surface plasmon supported by the metallic structure. However, this leads to suboptimal performance, even in the simplest sensor configuration based on the Otto geometry. We present a simplified coupled mode theory approach for evaluating and optimizing the sensing properties of plasmonic waveguide refractive index sensors. It only requires the calculation of propagation constants, without the need for calculating mode overlap integrals. We apply our method by evaluating the wavelength-, device length- and refractive index-dependent transmission spectra for an example silicon-on-insulator-based sensor of finite length. This reveals all salient spectral features which are consistent with full-field finite element calculations. This work provides a rapid and convenient framework for designing dielectric-plasmonic sensor prototypes-its applicability to the case of fibre plasmonic sensors is also discussed.

Keywords: coupled mode theory; directional coupling; fibre sensors; hybrid plasmonic waveguides; photonic integrated circuits; plasmonics; sensors.

Figure 1

Concept schematic of the challenge of calculating resonances in plasmonic sensors. (a) The simple Otto configuration relies on monitoring the reflectivity R of plane waves propagating in semi-infinite media as a function of angle $\theta$. At the angle ${\theta }_{\mathrm{SPP}}$ a SPP is excited. (b) $\theta$-dependent reflectance spectrum for $n_a=1$, $\lambda =800\mathrm{nm}$, and w as labelled. Also shown is the full colourmap of the reflectance as a function of $\theta$ and w for (c) $n_a=1$ and (d) $n_a=1.33$. Note that the spectral maps are subtly dependent on both $n_a$ and w.

Figure 2

Schematic of the HPWG sensor and the coupled mode theory picture. The modes in the dielectric and plasmonic regions, ${\psi }_1$ and ${\psi }_2$ respectively, couple linearly as described by Equation (6). The power in the dielectric at output is given by $T=|{\psi }_1{|}^2$. The periodic exchange of power between waveguides can lead to a resonant spectrum that in general depends on both the length of the device L and the analyte index $n_a$ [25].

Figure 3

Effective index $n_{\mathrm{eff}}=\beta /k_0$ as a function of wavelength for the geometry shown in Figure 2 when (a) $n_a=1.3$, (b) $n_a=1.4$, (c) $n_a=1.5$ in the lossless case. The dashed line shows the isolated plasmonic- and dielectric- modes, respectively. The solid lines show the hybrid eigenmodes. (d–f) show the associated calculated coupling coefficients, following the simple expression in Equation (8) (black line). Top row shows a schematic of the magnetic field for the plotted isolated- or hybrid-/super-modes.

Figure 4

Real part of the effective index $\Re e\left(n_{\mathrm{eff}}\right)=\Re e(\beta /k_0)$ as a function of wavelength for the geometry shown in Figure 2 when (a) $n_a=1.3$, (b) $n_a=1.4$, (c) $n_a=1.5$, using the lossy Drude model for the gold permittivity. The dashed line shows the isolated plasmonic- and dielectric- modes, respectively. The solid lines show the hybrid eigenmodes according to the “exact” solution (dark) and obtained from CMT via the eigenvalues of Equation (9) (light). (d–f) show the associated $\Im m\left(n_{\mathrm{eff}}\right)$.

Figure 5

Transmitted power by the plasmonic sensor as a function of $\lambda$ and $n_a$ for $L=10\mathsf{\mu }\mathrm{m}$ using (a) CMT, and (b) FEM. (c,d): same as (a,b) for $L=15\mathsf{\mu }\mathrm{m}$. (e,f): same as (a,b) for $L=20\mathsf{\mu }\mathrm{m}$. (g,h): same as (a,b) for $L=50\mathsf{\mu }\mathrm{m}$. EP: exceptional point.

Figure 6

Calculated colour maps of (a) $|{\beta }_1-{\beta }_2^R|/k_0+|\kappa -{\beta }_2^I/2|/k_0$ using CMT and (b) $|\widetilde{{\beta }_1}-\widetilde{{\beta }_2}|/k_0$ using the exact supermodes. The global minima in the phase space show the location of the exceptional point using our CMT model and the exact solution, as per Equations (10) and (11).

Figure 7

(a) Green (right axis): phase matching wavelength ${\lambda }_{\mathrm{PM}}$ where ${\beta }_1={\beta }_2^R$, and associated half beat length $L_b$ according to the supermodes obtained with CMT (orange) and “exact” calculations (blue). (b) Associated absorption length $L_a$. Solid lines indicate the average $L_a=(L_a^1+L_a^2)/2$; shaded regions encompass the $L_a^1$ and $L_a^2$ boundaries.

Figure 8

(a) Transmission spectrum using the “conventional” approach of Equation (14), as a function of wavelength, for the three analyte indices as labelled, using $L=10\mathsf{\mu }\mathrm{m}$. Also shown are the resonant wavelength ${\lambda }_R$, corresponding to the spectral minimum and the $\delta \lambda$, corresponding to the FWHM. (b) Associated ${\lambda }_R$ vs. $n_a$ (green circles, left axis), second order polynomial fit (green line), and resulting sensitivity S (orange line, right axis.) Also shown in (c) are the $\delta \lambda$ vs. $n_a$ (orange curve, left axis) and the total FOM = $S/\delta \lambda$. (d–f): same as (a–c), obtained from the CMT approach, using a subset of the data shown in Figure 5a as labelled. (g–i): same as (d–f), obtained from FEM calculations, using a subset of the data shown in Figure 5b as labelled.