Extension of the bright high-harmonic photon energy range via nonadiabatic critical phase matching

Abstract

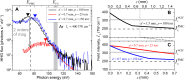
The concept of critical ionization fraction has been essential for high-harmonic generation, because it dictates the maximum driving laser intensity while preserving the phase matching of harmonics. In this work, we reveal a second, nonadiabatic critical ionization fraction, which substantially extends the phase-matched harmonic energy, arising because of the strong reshaping of the intense laser field in a gas plasma. We validate this understanding through a systematic comparison between experiment and theory for a wide range of laser conditions. In particular, the properties of the high-harmonic spectrum versus the laser intensity undergoes three distinctive scenarios: (i) coincidence with the single-atom cutoff, (ii) strong spectral extension, and (iii) spectral energy saturation. We present an analytical model that predicts the spectral extension and reveals the increasing importance of the nonadiabatic effects for mid-infrared lasers. These findings are important for the development of high-brightness soft x-ray sources for applications in spectroscopy and imaging.

Fig. 1.. Illustration of the general concept.

(A) Illustration of the nonadiabatic HHG process driven by an intense few-cycle pulse in a gas cell, which exhibits the effects of plasma-induced intensity decay, temporal pulse reshaping, and variation of gas ionization along z. The HHG spectrum is the integrations of the emitters along z under a varying driving field. Inset: Illustration of the modulation of electron trajectories owing to the nonadiabatic field temporal reshaping. The solid line represents the incident driving laser field. The dashed line represents the field profile deformed by the nonadiabatic effects. The microscopic electron trajectories under two different driving fields are illustrated. (B) Illustration of the gas ionization fraction at the pulse temporal center, and the relationship among the critical intensities (IcPMC and IcNCIF ), critical ionization fractions (ηcPMC and ηcNCIF ), and the HHG photon energies (E_PMC and E_1%). (C to E) HHG spectrum driven by pulse durations of τ = 9, 22, and 170 fs, respectively, under different laser intensities (I_L). (F to H) Results of numerical simulations under similar conditions as in (C) to (E). a.u., arbitrary units.

Fig. 2.. Influence of nonadiabatic effects on harmonic spectrum.

(A) Temporal field shapes obtained from the numerical simulations at the entrance and the exit of a gas cell (d = 1.5 mm) under laser intensity of I_L = 200 TW cm⁻². The gas cell is filled with argon with the pressure (p) of 100 torr. The time for the peak field is labeled by the solid triangles. (B) Same as (A) for I_L = 700 TW cm⁻². (C and D) Time-frequency analysis of the HHG generated under the laser conditions in (A) and (B). The emission time for the highest harmonic orders are labeled by the solid triangles. (E) Experimental HHG spectrum in argon driven by different laser intensity I_L with d = 1.5 mm and p = 50 torr. The pulse duration is τ = 9 fs. The blue dashed line represents E_cutoff when IL<IcPMC and a constant when above IcPMC . The yellow dashed-dotted line represents ΔE_qt + E_cutoff when IL<IcNCIF and a constant when above IcNCIF . Three regimes are distinguished by the two critical intensities (IcPMC and IcNCIF ). (F) Same as (E) obtained from the numerical simulations under the same conditions.

Fig. 3.. The NCIF model results.

(A) Results of the NCIF model for HHG in argon under different pulse durations (τ). The solid lines are the results of Eq. 5, with C_d = 0.35 (red, green, and blue) and C_d = 0 (black). The dashed lines are the results of Eq. 6. The intersections are labeled by open symbols. The open triangles label the results for PMC, and the open squares are for the 1%-intensity energy. (B) Comparison between the experimental results of EPMCsat (open triangles), E1%sat (open circles), and the NCIF model results (solid and dashed lines) in argon. The shaded area represents the variation of EPMCsat and E1%sat under different CEP phases (Δϕ_CEP). Inset: The illustration of the driving field waveforms under different Δϕ_CEP, with peak-field time labeled. (C) Same as (B) for the results in krypton. (D) NCIF model results under different wavelengths (λ_L) in argon, neon, and helium. The symbols represent the results obtained from the numerical simulations. (E) Typical numerical spectrum of HHG in neon. The E_PMC and E^1% are labeled. The gas pressure is 100 torr, the cell length is 1.5 mm, and the driving intensity is 1000 TW cm⁻².

Fig. 4.. The nonadiabatic spatial integration effects.

(A) HHG spectrum in argon obtained under different gas-cell lengths (d) and gas pressure (p). The driving intensity I_L is fixed to be 400 TW cm⁻² and the pulse duration τ = 9 fs. The energy of E_PMC is labeled by solid triangles. (B) Peak intensity of the driving field as a function of the propagation distance in the gas cell (z), obtained from the numerical simulation. The critical intensities are labeled for τ = 9 fs, λ_L = 1030 nm in argon, obtained from the NCIF model. (C) Same as (B) for different d and p.