A framework for reconstructing transmission networks in infectious diseases
- PMID: 36567737
- PMCID: PMC9761645
- DOI: 10.1007/s41109-022-00525-4
A framework for reconstructing transmission networks in infectious diseases
Abstract
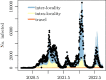
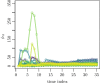
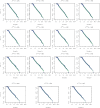
In this paper, we propose a general framework for the reconstruction of the underlying cross-regional transmission network contributing to the spread of an infectious disease. We employ an autoregressive model that allows to decompose the mean number of infections into three components that describe: intra-locality infections, inter-locality infections, and infections from other sources such as travelers arriving to a country from abroad. This model is commonly used in the identification of spatiotemporal patterns in seasonal infectious diseases and thus in forecasting infection counts. However, our contribution lies in identifying the inter-locality term as a time-evolving network, and rather than using the model for forecasting, we focus on the network properties without any assumption on seasonality or recurrence of the disease. The topology of the network is then studied to get insight into the disease dynamics. Building on this, and particularly on the centrality of the nodes of the identified network, a strategy for intervention and disease control is devised.
Keywords: Autoregressive model; Betweenness centrality; COVID-19; Network reconstruction; Optimal control.
© The Author(s) 2022.
Conflict of interest statement
Competing interestsThe authors declare that they have no competing interests.
Figures








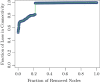
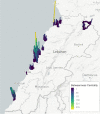
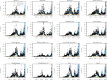
References
LinkOut - more resources
Full Text Sources
