Field and intensity correlations: the Siegert relation from stars to quantum emitters
- PMID: 36568919
- PMCID: PMC9763155
- DOI: 10.1140/epjd/s10053-022-00558-5
Field and intensity correlations: the Siegert relation from stars to quantum emitters
Abstract
The Siegert relation relates field and intensity temporal correlations. After a historical review of the Siegert relation and the Hanbury Brown and Twiss effect, we discuss the validity of this relation in two different domains. We first show that this relation can be used in astrophysics to determine the fundamental parameters of stars, and that it is especially important for the observation with stellar emission lines. Second, we check the validity of this relation for moving quantum scatterers illuminated by a strong driving field.
© The Author(s) 2022.
Figures

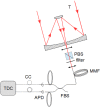

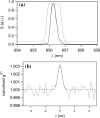
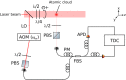
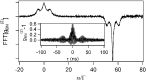

References
-
- Wiener N. Generalized harmonic analysis. Acta Math. 1930;55:117–258. doi: 10.1007/BF02546511. - DOI
-
- Khintchine A. Korrelationstheorie der stationären stochastischen prozesse. Math. Ann. 1934;109(1):604–615. doi: 10.1007/BF01449156. - DOI
-
- Glauber RJ. The quantum theory of optical coherence. Phys. Rev. 1963;130:2529. doi: 10.1103/PhysRev.130.2529. - DOI
-
- Siegert AJF. On the fluctuations in signals returned by many independently moving scatterers. Report: Radiation laboratory, Massachusetts Insitute of Technology; 1943.
-
- G. Maret, P.E. Wolf, Multiple light scattering from disordered media. The effect of brownian motion of scatterers. Zeitschrift für Physik B Condensed Matter. 65(4), 409–413 (1987). 10.1007/BF01303762
LinkOut - more resources
Full Text Sources
